previous        table of contents        next

---

CHAPTER IV

CONSTRAINTS ON PROVING

                    “I know what your thinking about,” said Tweedledum; “but it isn’t so, nohow.”
                    “Contrariwise,” continued Tweedledee, “if it was so, it might be, and if it were
                      so, it would be; but as it isn’t, it ain’t. That’s logic.”
                                                                                        — Lewis Carroll, 
                                                                                             Through the Looking Glass, and What Alice Found There.

My research would be much more simple if the same needs always led to the same reasoning.  If exploring meant proving, and verifying meant reasoning inductively, and explaining meant reasoning by analogy, then the need to prove would be all that needed to be said about it.  Unfortunately, the examples in the previous chapters show that this is not so.  In addition to the needs that motivate proving there are also other factors that constrain proving.  In Chapter II these constraints are mentioned as they occurred, but the focus of that chapter is needs, and so constraints are not treated systematically there.  This chapter attempts to organize what I learned about three important constraints on proving into a useful summary.

1. Individual differences

Not everyone proves in the same way.  It would be foolish to try to generalize from a few people’s proving behaviors to a larger group.  In the case of the participants in my studies there is ample evidence of considerable variation in proving style and in the needs felt (see Appendix D for a summary of this variation).  In the previous chapter I described Stacey and Kerry’s approaches to the Arithmagon in which there are clear differences between them as individuals.  In this section I will describe two other participants, Bill and John, in order to further illustrate the range of activity I observed.

Bill and John were two students in a Math 13 class at North School.  Math 13 is the grade 10 mathematics class in which students who have done poorly in grade 9 find themselves placed.  Bill was among the better students in his class and seemed to be actively engaged in following the teacher’s lessons and in doing the assigned work.  He responded readily to the teacher’s questions and asked questions if he did not understand something.  John was more quiet but also seemed to be actively following the lessons.  He did have difficulty with the assigned exercises on some occasions and was more likely to turn to Bill for help than to ask the teacher. 

Bill and John were not only different in many ways from the other participants in the studies (as one would expect given the differences between the Math 13 program and undergraduate mathematics) but also different from each other.  At the same time the proving they did is similar in many ways to that done by other participants.

Bill explored generally toward some goal and explained both to himself and to John but verified only by making reference to my authority.  In his explorations he made use of both unformulated proving and inductive reasoning.  He had a preference for an explanation by analogy for the sum of two odd numbers being even but on other occasions accepted unformulated and formulated proving as explanation.  He was the only participant in the study to explicitly reject inductive verification, accepting verification by authority only.

Bill’s spontaneous efforts at proving to explain or explore were generally short and unformulated.  When I guided him through more formulated proving however, he displayed a clear understanding of the arguments and, in the case of the formula we deduced for the Arithmagon he accepted the proving as explaining.  While proving is something Bill is capable of, at least unformulated proving, it is not his first choice for satisfying a need to explain, explore or verify.  In explaining the fact that two odd numbers always add up to an even number, he preferred his analogy to the product of two negative numbers to either of the pre-formal proofs we produced.  In that case he explicitly said he did not like explanations like the pre-formal proofs.  In the case of the formula for solving Arithmagons, he had said he preferred the form of the formula which made it easy to explain how it worked.  This seeming contradiction illustrates the importance of the need to prove.  In the case of the Arithmagon formula we were dealing with a new piece of mathematics, which lacked an explanation.  In the case of the sum of two odd numbers, Bill had provided an explanation by analogy, and had it on my authority that the rule was a general one.  There was no need for proving the rule. 

In exploring Bill was like the other participants in preferring to explore inductively.  In verifying he was quite different.  Most of the participants would use either inductive reasoning or proving to verify.  In Bill’s case reasoning did not verify.  He relied completely on my authority to establish truth.  This was strongly suggested by Bill’s reaction when I claimed that 117 digit odd numbers do not generally add up to even numbers.  Bill responded, “I don’t see how come that is, ... but that’s really kind of neat.”  Against my authority, two pre-formal proofs, an analogy, and a wealth of inductive evidence were insufficient to convince Bill.

John was less involved and less vocal than Bill and so there is less that can be said about his reasoning.  He explored inductively but whether he had a goal in mind was not clear.  He explained when asked to, and asked for explanations from Bill.  Explaining by proving was acceptable to him, and he used proving to explain in simple situations. His verifying was tentative, but he was more willing than Bill to accept inductive verifications.

The clearest indication of John’s thinking came after Bill and I had deduced a formula for the Arithmagon: (A+C)-(A+B)-(B+C) / 2 (MAT episodes 10-14).  Our formula involves variables representing the three unknown corners, grouped in added pairs according to sides.  For Bill this formula was good because it had explanatory power.  While he recognized this power, John preferred a different formulation: E-D+F / 2.   This formula is easy to use.  John choice of formula illustrates his preference for mathematics that is easy to use, as opposed to mathematics that is easy to understand.

Summary

While the cases of Stacey and Kerry (described in the previous chapter) and Bill and John do not begin to cover the range of individual differences seen in the participants in my studies, they do point out certain kinds of differences that influence the need to prove and the proving that is done.  An important difference between Stacey and Kerry was in what they knew, or at least the technical skills with which they felt comfortable.  Kerry’s use of mechanical deduction could not have occurred if he had been unfamiliar with solving systems of equations and might not have occurred if he had been just as proficient but less comfortable.  Table 2 shows the initial method used to solve the original puzzle for all the participants in the studies, and whether they had been taught to solve systems of equations.  The entries “10+” and “10–” indicate the accelerated Math 10 program at South school, and the Math 13 class at North School, respectively.  The cases marked with a question mark (?) were in the process of learning to solve systems of equation at the time of the Arithmagon session, and it is not clear exactly what they had been taught at the time of the session.

 

Group	Grade	Solution method	Taught?
Ben & Wayne	U	Trial and Error	Yes
Jane & Chris	U	System of Equations	Yes
Kerry & Stacey	U	System of Equations	Yes
Eleanor & Rachel	U	System of Equations	Yes
Roger & Marie	U	Trial and Error	Yes
Trisha & James	U	Trial and Error	Yes
Laura & Donald	U	Trial and Error	Yes
Colin & Anton	12	System of Equations	Yes
Joseph, Stephen, & Scott	10+	System of Equations	Yes
Alec & Darrell	10+	System of Equations	Yes
Tara & Topaz	10+	Trial and Error	?
Ann, Lynda, & Joanna	10+	Trial and Error	?
Bill & John	10–	Trial and Error	No
Sandy	6	Unformulated proving	No

Table 2: Use of systems of equations in solving the Arithmagon.

Bill and John indicate the importance of individual’s beliefs about mathematics and learning to the need to prove.  Bill’s reliance on authorities as the ultimate source of verification limited the importance of that need in motivating both proving and inductive reasoning.  While proving to verify is not common in general, most of the participants in the studies did verify inductively, and Bill’s reluctance to do so may be limiting his possibilities for learning from his own experiences.  John’s preference for useful mathematics over explanations could make learning mathematics more difficult for him.  It provides him with a disincentive to develop relational understandings as opposed to instrumental understandings (to use terminology from Skemp, 1987).  Instrumental understandings are not as useful a basis for learning new concepts as relational understandings and are harder to maintain.

2. Social constraints

In all the sessions the participants worked in a social context.  The observers and the other participants defined an environment in which each participant reasoned.  In my final chapter I describe a theory in which the development of deductive reasoning is tied to social relations between people, mediated by language.  If deductive reasoning develops out of social relations then it is not surprising that reasoning in problem solving is constrained by social factors.  In this section I will describe how social constraints were linked to proving activities in the cases of Rachel and Eleanor, two university students, and Bill and John, two Math 13 students.

Eleanor and Rachel

Eleanor and Rachel provide an excellent example of social constraints, in part because of their manner of working together and in part because of the different social contexts in which they worked.  The Fibonacci session was their first session.  In it they established a pattern of working somewhat independently but consulting each other regularly.  This permitted them to act independently when they wished but also to work with each other’s ideas.  In the Arithmagon session they worked with Ben and Wayne, but the dynamic between them was similar to that they established in the Fibonacci session.  Other social constraints, however, meant that they acted quite differently in the two sessions.

Rachel

Rachel spent the Fibonacci session exploring and verifying the conjectures she made inductively (see MAT).  She noticed a pattern in the sequence of every third Fibonacci number, which she then described to Eleanor.  Eleanor formalized the pattern as F_3n = 4F_3n-3 + F_3n-6.  For example, F₉ = 34, F₆ = 8, and F₃ = 2, and 34 = 4(8) + 2.  Rachel continued to explore inductively, looking for similar patterns for F_4n, F_5n, F_6n, etc.  Whenever she found a pattern she described it in terms of actions, e.g., “Multiply by 4, add the previous one, and you get the next one.”  She then helped Eleanor formalize her pattern, or in the case of the later patterns, formalized it herself.  This pattern of discovery, verification and formalization was her way of working throughout the session.

In the Arithmagon situation, Rachel was sitting between Eleanor and Tom Kieren, who was observing.  She began by solving the puzzle using a system of equations, and then began looking for patterns, exploring inductively as she had in the Fibonacci situation.  She interrupted her explorations to listen to Ben describe his method of solving by systematic trial and error.  She then attempted to use his method.  When I suggested to Ben that he try to solve a 1-4-12 triangle (because his method would need to be modified to solve it) Rachel also attempted to solve that triangle.

About halfway through the session, Rachel’s activity changed (MAT episode 8).  She stopped exploring inductively and began using formulated proving to explore special cases of the problem (e.g., when two sides are equal).  Her explorations are described in Chapter II, section 2.  In the interview session I asked her why she had begun to explore in this way. 

(1) DR: Why were you doing that?

(2) Rachel:

Oh, you want me to answer right now? [laughter] Because I was stuck at them.  I didn’t know where to go.  And Tom was sitting beside me saying, “Well, what can you do now?”

(3) Eleanor:      Nothing, nothing.  [laughter]

(4) Rachel:

So I was thinking I’d better think of something, or else that question’s going to keep coming.  So I just thought, well hey, in math you always get that right?.  You always get those conditions. Every teacher’s listing these conditions.  Now, if we have this condition where this equals that. You know what I mean. So that’s. It just.  You know.  It comes from my head.  Something I knew of already that I thought I could apply to that problem.

At first, Rachel had addressed her need to explore by way of inductive reasoning, but the presence of Tom was a social constraint that led her to use formulated proving.  A bit later, Tom became a more explicit social constraint, by suggesting that she see what she could derive for the general case.  This led to her derivation of a general formula for solving the Arithmagon. 

Eleanor responded to Rachel’s announcement of her formula by asking for an explanation.  This social context led to a need to explain, and Rachel’s immediate history of formulated proving led her to use formulated proving to explain in this context. 

Eleanor

In the Fibonacci session Eleanor played off Rachel’s ability to see patterns by formalizing them, and then searching for patterns in the formalization.  Without Rachel’s participation her activities would have been different, since her focus would have had to include the original sequence as well as the relations Rachel found in it. 

In the Arithmagon situation Eleanor was sitting between Rachel and Ben.  She began solving the original puzzle using a system of equations and then stopped when she saw that Rachel had found the answer.  After comparing methods with Ben and Wayne she then began trying to use Ben’s method to solve the triangle.  When I proposed the 1-4-12 triangle she discussed with Ben whether it was possible or not, and then, at Ben’s request, solved it using a system of equations.  She then joined Ben and Wayne in exploring inductively.  They found the relations A+a = B+b = C+c and a+b+c = 2(A+B+C).  Eleanor then worked independently, eventually discovering a general method of solution based on these relations.  Her method is described in Chapter II, section 1 and in Appendix E.  After Rachel announced her formula and explained its derivation to Eleanor, Eleanor described her method, and began explaining, to herself for the most part, how it related to Rachel’s formula. 

Eleanor changed the way she was working depending on the way the people around her were working.  She used mechanical deduction while Rachel was doing so.  She tried Ben’s method, and solved a triangle with a system of equations when Ben asked her to.  She explored inductively when working with Ben  and Wayne, who had been working inductively (and, in Wayne’s case, by analogy) all along.  She explored using unformulated proving when working alone and then explained using formulated proving when working with Rachel. 

Bill and John

Bill and John are included here because of the contrast between their inductive and analogical reasoning in the two problem sessions, compared to their use of formulated proving in the interview sessions when I encouraged them to reason deductively.  In the problem sessions they occasionally used unformulated proving, but it required the social context of my encouragement for them to formulate their proving, and to prove for extended periods.  This is heartening in terms of the potential influence a teacher has on students’ reasoning.  The proving they did in the interview sessions is described in Chapter II, section 1.

3. The prompts

The factor that might have been expected to have an influence of the participants’ proving, the problems they were investigating, did turn out to constrain the activities in which they engaged.  Investigations of the Arithmagon problem involved proving, and especially mechanical deduction, more often than either of the other two situations.  In the GEOworld situation almost all the activity was inductive exploration.  In the Fibonacci situation, some participants did nothing but inductive exploration while others engaged in some, usually unformulated, proving.

Arithmagon

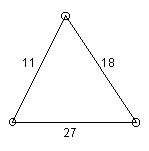
Figure 30: The Arithmagon prompt.

The Arithmagon problem was chosen for its potential to be generalized in many ways, and the variety of solution methods and interest it created in informal pilot testing of it.  In the studies it lived up to my expectations, and in some cases it occasioned truly unexpected mathematical activity (see Appendix E).  The discovery that other researchers (Simpson, 1994; Duffin & Simpson, 1993) were also using the problem for research into proof was fortuitous and added another point of view to my research.

All the participants in the studies investigated the Arithmagon.  The activities in which they engaged ranged from inductive exploration to formulated proving.  Some participants discovered a general method for solving Arithmagons, some discovered a formula, some did both, and some did neither.  The activities of all the participants in my studies is summarized in Table 3.

The variety of solution methods listed in Table 3 only begins to suggest the openness of the Arithmagon situation.  For example, Kerry and Stacey’s general method for solving Arithmagons, based on adding a new triangle around the original, is very different from Eleanor’s method of adding the sides together, dividing by 2, and using this number, which is also the sum of a side and the corner opposite it, to find the corners.  Appendix E lists a number of other methods of solving the original puzzle and deriving a general method.

Group	Solution method	Means of deriving a general method or formula
Ben & Wayne	Inductive	Told by Rachel
Jane & Chris	Mechanical deduction	None
Kerry & Stacey	Mechanical deduction	Inductive
Eleanor & Rachel	Mechanical deduction	Formulated proving
Roger & Marie	Inductive	Guided proving
Trisha & James	Inductive	Inductive
Laura & Donald	Inductive	Inductive
Colin & Anton	Mechanical deduction	Mixed inductive and deductive reasoning
Joseph, Stephen, & Scott	Mechanical deduction	None
Alec & Darrell	Mechanical deduction	None
Tara & Topaz	Inductive	Inductive
Ann, Lynda, & Joanna	Inductive	None
Bill & John	Inductive	Guided proving
Sandy	Formulated proving	Formulated proving

Table 3: Summary of participants’ activities in the Arithmagon situation.

Fibonacci

Figure 31: The Fibonacci prompt.

The Fibonacci numbers are famous as a rich source of patterns, all derived from a simple rule.  In my research for my master’s thesis (Reid, 1992), I found that the pattern of every third Fibonacci number being even was easily discovered and proved.  For this reason I included the Fibonacci situation in my research for this dissertation.  Surprisingly, the pattern of every third Fibonacci number being even was either too simple (some participants noticed it but continued looking for something more significant) or missed entirely.  One unexpected outcome was the 

discovery, by several participants, of a relation between every third Fibonacci number which was new to me.  Rachel’s discovery of it is described above (section 2).  The wording of the prompt caused some trouble, and it was changed for each of the three studies for which it was used, but in all cases the presence of several suggestions for patterns to notice led to participants moving quickly on from one inductive exploration to the next.  This fragmented pattern of exploration is described in more detail in Kieren, Pirie, and Reid (1994).  The Fibonacci situation was not used at South School because of this problem.

My chief expectation for the Fibonacci situation was that the participants would notice that every third Fibonacci number is even, and prove this, noting that the rule defining the sequence forces a pattern of Odd, Odd, Even, Odd, Odd, Even, onto the sequence.  While this pattern was noticed in several cases, it was only Kerry and Bill who proved the pattern, and in both cases it was as a result of an observer’s intervention.  What I had expected to be an occasion for proving to explain became an occasion for proving in a teacher-game.

GEOworld

The GEOworld offered the possibility of seeing the participants prove from postulates of their own creation, as a way of exploring and explaining.  The situation is similar to a scientific investigation, as initial theories must be established inductively, but then proving can be used both to test the theories, and to explore in a more directed way.  None of the participants did anything in the GEOworld situation other than exploring inductively and occasionally making a prediction and testing it.  To allow additional time for interviews, the GEOworld situation was not used at North School.

Summary

The sampling of examples in this dissertation reveals that the Arithmagon situation was much more conducive to proving than either the Fibonacci situation or GEOworld.  That some situations are better for proving than others is not a surprise, but the exact features that made the Arithmagon different are not entirely clear.  It was important that the situation gave some initial relations on which to build deductive arguments, which GEOworld did not do.  The imprecision of the prompt, compared to the Fibonacci prompt, may also have been an advantage. 

It should be noted, however, that having a problem situation conducive to proving is not enough.  As has been pointed out above, social and personal factors are also important, and the variety of activities in which participants engaged in the Arithmagon situation is an indication of this.