previous table of contents next
CHAPTER III
KERRY, STACEY AND THE ARITHMAGON: REASONING IN ACTION
I gave her one, they gave him two,
You gave us three or more;
They all returned from me to you,
Though they were mine before.
— Lewis Carroll,
Alice’s Adventures in Wonderland.
In this chapter I will describe the reasoning of a pair of undergraduate students, Stacey and Kerry, as they investigate the Arithmagon situation. The terms I introduced in the previous chapter will be used in this description, clarifying the relationships between needs and proving, while presenting a more situated view of students’ proving.
Stacey was a student in mathematics education when she volunteered to participate in the first clinical study. She asked if she could work with her friend, Kerry, who was an undergraduate student in Finance. It was plain in the problem solving sessions, and I hope it will be clear in the transcripts given below, that Stacey and Kerry enjoyed investigating the situations, and were comfortable working together. They investigated the Arithmagon in their first problem session. They were interviewed three weeks later, after investigating the other two problem situations.
The numbers on the sides of this triangle are the sums of the numbers at the corners. Find the secret numbers.
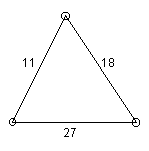
Generalize the problem and its solution
Figure 24: The Arithmagon prompt.
1. Mechanical deduction to explore*
After Stacey and Kerry were given the Arithmagon prompt (Figure 24) they negotiated how begin. The operant need at this point is a need to explore towards
* The numbers of the sections in this chapter correspond to MAT episode numbers in Stacey and Kerry’s MAT for the Arithmagon in Appendix C.
the specific goal of finding an answer to the puzzle. Stacey proposed exploring inductively, by “trial and error” (line 2). Kerry rejected this suggestion, preferring to “deduce” the answer by mechanical deduction, using a system of equations (line 8).
(1) Kerry: I guess this is uh, — uh
(2) Stacey: Trial and error?
(3) Kerry: No. We’ll go. Let’s assign variables to these then. Do you want? We can write on this paper right?
(4) DR Sure
(5) Stacey: Go for it
(6) Kerry: We’ll start with A B and C.
(7) TK: We’ve got plenty of paper
| (8) Kerry: | OK. Yeah. And I guess we’ll probably get a system of equations out of that. And we’ll try and- And we’ll subtract one equation from the other. And try and deduce one variable, plug it back in — OK So that’s the sum of A and B. |
(9) Stacey: Yup.
(10) Kerry: OK [Kerry starts writing equations]
(11) Stacey: A and B is 11. B and C is 18. And A and C is 27 —
(12) Kerry: OK — These are our three formulas. Our three equations.
After solving the equations they checked their answer against the original puzzle, verifying the result of a mechanical deduction by simple, unformulated proving. Kerry then noted the general rule that if the system of equations gave a solution, then the answer must work in the original puzzle. This is a second case of proving to verify, specifying from a general rule in a formulated way. In both cases the proving involves only a single deductive step, and is applied to a very simple situation.
2. Unformulated proving to explore
Stacey then began exploring again, this time without a clear goal (this episode is also described at the beginning of Chapter II).
(1) Stacey: What happens if you add the middle numbers together? —
(2) Kerry: Well I guess we could, hmm.
(3) Stacey: I just want to try something. If you take 27, 18, and 11. 2, 4, 5, 56. Right?
(4) Kerry: Sure.
| (5) Stacey: | And you have — So you add each of those twice, right? — Yeah you do. That’s not going to help you either. That’s what you end up doing right? |
(6) Kerry: What’d you do?
(7) Stacey: You add A, B, C. Then you multiply them by 2. You get this answer. —
(8) Kerry: Do you add?
(9) Stacey: 22, and 34. Yup. Do you know what I mean?
| (10) Kerry: | Sorry. So you add this and multiply by 2 so, like, the sum of this is 28 times 2. And it’s 56. Good one. What’s that mean? |
(11) Stacey: Nothing. [laughing]
(12) Kerry: Is that-
(13) Stacey: That was just-
(14) Kerry: Is that true for all of them?
(15) Stacey: Yeah.
(16) Kerry: I guess so. It must be. It can’t just be fluke.
Stacey, in lines 1 through 5, is exploring, as indicated by her initial comment “What happens if you add the middle numbers together?” She continues, proving in an unformulated way. After determining the sum of the three numbers (56, line 3) she reasons that each of the secret numbers must be included in the sum twice. This occurs because “you add each of those twice,” “those” being the secret numbers. Although she does not see any connection with her conclusion and the problem of generalizing the Arithmagon, she checks with Kerry to see if he has followed her reasoning (line 5). Because it is unformulated, he has not understood either her conclusion, or how she reached it (line 6).
She manages to communicate her conclusion in the specific case that they are considering (lines 7-10), at which point Kerry asks “Is that true for all of them?” provoking a need to verify. Stacey’s unformulated proving, although it was originally begun to satisfy a need to explore, also satisfies this new need to verify but only for her. Kerry, who has no access to her unformulated reasoning, instead verifies by a probabilistic argument, based on the inductive evidence that most patterns observed in mathematical situations turn out to be general patterns, rather than “flukes.”
An important aspect of this case is the ease with which Stacey’s conclusion was forgotten. When Stacey and Kerry were searching for an explanation for the division by 4 in the method the discovered later in the session (see section 9 or Appendix E), they made no link between the relation Stacey discovered and the division by 4. Given their failure to come up with any explanation other than a weak analogy, it would be surprising if they remembered Stacey’s relation but failed to make use of it. Kerry, in fact, claimed in the interview session that he had never even seen Stacey’s relation.
3. Mechanical deduction to explore
After dismissing Stacey’s relation between the sum of the sides and the sum of the secret numbers, Kerry proposed solving the puzzle again, using a matrix instead of a system of equations. This is another example of mechanical deduction used to explore, but as the solution to the puzzle was already known to them, this
exploration must not have had that as its goal. Instead Kerry was exploring to find something new, without any idea of what it might be.
While Kerry seemed comfortable working with his matrices, and was proceeding in a mechanical way, Stacey seemed uncomfortable, and as Kerry worked she interpreted the matrices as equations. This became evident when Kerry made an arithmetic error resulting in the matrix:
1 1 0 11
0 1 1 18
0 0 1 12
Kerry saw nothing significant in this matrix, but Stacey, who was interpreting Kerry’s mechanical deduction saw 0 0 1 12 as C=12, which she knew contradicted the value for C they had found earlier. This reveals an important aspect of mechanical deduction, that the meaning of the symbols being manipulated is suspended which the deduction proceeds.
After Stacey pointed out the contradiction, they carefully checked Kerry’s calculations but did not find the error. They were uncertain what to do next, but eventually they continued reducing this matrix, arriving at a second solution to the Arithmagon. The existence of this second solution made them aware of an implicit assumption they had made, that only one solution existed. They then checked their new solution against the original puzzle (verifying by a short, unformulated act of proving) and rejected it, concluding that they had made an error somewhere in the reduction of the matrix. Kerry ended this episode by specifying from the (false) generalization that reducing a matrix gives a unique solution if the number of variable equals the number of equations.
4. “Generalizing”
Turning to the cryptic instruction “Generalize the problem and its solution” they were uncertain what to do. Kerry decided that generalizing meant describing what they had done in solving the system in general terms (e.g., “We added the first two equations.”) This rehashing of their actions is not described as reasoning in my terminology, although it could be considered a kind of formulating of the rules of their mechanical deduction.
5. Inductive and deductive exploring
This is another episode of Stacey exploring, this time involving a mixture of unformulated proving, mechanical deduction, and inductive reasoning. As Kerry was winding up his “generalization” Stacey had been looking thoughtfully at the original problem. As soon as he finished, she began exploring:
| (1) Stacey: | OK. This is what we have. — — 18 11 and 27 and we’re given three other numbers. — Right? What can we do with three other numbers? We can, extend lines. — — — |
(2) Kerry: What’ya doing? Making another big triangle?
(3) Stacey: Yeah. — I don’t know what I’m doing yet. ... And we’ll call— What’s 11, 27? Right. This one. What was this? 10?
(4) Kerry: Yeah. Let’s get rid of this. The other answers
(5) Stacey [laughs] Well what-
(6) Kerry: This, this was 17. And, what, what was this?
(7) Stacey: It was-
(8) Kerry: This side here was
(9) Stacey: 17
(10) Kerry: C, was 17. Yeah.
(11) Stacey: And this is 17. What was the top one? 1.
(12) Kerry: 1. —
Here she begins exploring, without a goal: “I don’t know what I’m doing yet.” She adds a second triangle around the original one, and fills in the values which they now know on her new diagram (see Figure 25). The “other answers” Kerry refers to in line 4 are the values obtained from their matrices.
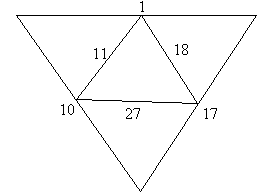
Figure 25: Stacey’s triangle with “extended lines.”
(13) Stacey: You keep going.
(14) Kerry: Where you going?
(15) Stacey: You keep going. We could find numbers for this. —
(16) Kerry: For that?
(17) Stacey: Yeah. —
(18) Kerry: OK. So you want to solve that then?
(19) Stacey: Umhmm
(20) Kerry: OK.
(21) Stacey: It will go right to zero. —
(22) Kerry: Are you saying-
(23) Stacey: This I don’t, I don’t know.
(24) Kerry: Are you saying the numbers would keep getting smaller?
(25) Stacey: Yeah, these ... would have to be-
(26) Kerry: Yeah I guess the will be getting smaller
(27) Stacey: -like decimals. ‘Cause you got 1 on one side. — ...
Stacey proposes here that they solve the new 1-10-17 triangle revealed by her diagram. This generation of new data about triangles is part of exploring by inductive reasoning. At the same time her prediction “It will go right to zero” is arrived at by unformulated proving, possibly based on her earlier conclusion (in episode 2) which implies that the sum of the sides will be halved for each new triangle she adds by “extending lines.” As the sums must have a limit of zero, she reasons that the individual numbers on the sides must also have the same limit, and that eventually they “would have to be ... decimals.” This is likely to happen soon, as “you got 1 on one side.”
(28) Kerry: You, want, you want to try to solve it then?
(29) Stacey: Yeah sure, Away you go. ...
(30) Kerry: OK, then let’s label it.
(31) Stacey: I like drawing it
(32) Kerry: OK, well label these anyways. So we’ve gone. So go. D E
(33) Stacey: and F
(34) Kerry: F. OK. D plus F equals 10. D plus E equals 1. E-
(35) Stacey: E plus F
(36) Kerry: plus F
(37) Stacey: 17
(38) Kerry: Equals 17 — OK So uh,
(39) Stacey: ... How are we doing here?
(40) Kerry: OK, we’ll subtract, we’ll take uh,
(41) Stacey: 1 minus 2
(42) Kerry: 1 minus 2. So we’ve got
(43) Both: F minus E is 9
(44) Kerry: and then we’ll go, uh.
(45) Stacey: That plus 3
(46) Kerry: Hmm?
(47) Stacey: Plus 3
(48) Kerry: Plus 3?
(49) Stacey: Yeah.
(50) Kerry: OK. E plus F equals 17 and then cancel, cancel. 2 F equals 26
(51) Stacey: F equals 13.
(52) Kerry: 13
(53) Stacey: So it’s 13 here.
(54) Kerry: 13 there. And, want another one?
(55) Stacey: Yeah.
(56) Kerry: OK. Then . Oh I think we’re going to get a nice negative number.
(57) Stacey: Oooh
(58) Kerry: D equals minus 3 —
(59) Stacey: Negative 3 and E is then
(60) Kerry: E is
(61) Stacey: [whispers “4”]
(62) Kerry: [whispers “4”]
(63) Stacey: Sorry. 4. [laughs]
(64) Kerry: OK. So we got. We did get a negative number.
This long recital is the spoken manifestation of mechanical deduction. Throughout it is Kerry who writes the equations, although Stacey is involved in what he does. Note that the equations are referred to by numbers (lines 41, 42, 45, 47, and 48). They are being added as formal strings, although Stacey is using some aspects of their structure to decide which ones to add first. At line 54 Kerry continues to work with the equations, in spite of the fact that knowing one secret number means that they could return to the meaningful situation of the triangle to find the rest of the values. Because the meanings of the equations have been suspended while doing the mechanical deduction, there is no prompt for him to return to the original situation. Stacey is connecting what Kerry is writing to the original triangle, and when she whispers the final value, 4, she has seen the answer in the triangles rather than in the equations. Her apology in line 63 is directed towards the observers, who have asked them to speak clearly to make deciphering the videotape easier.
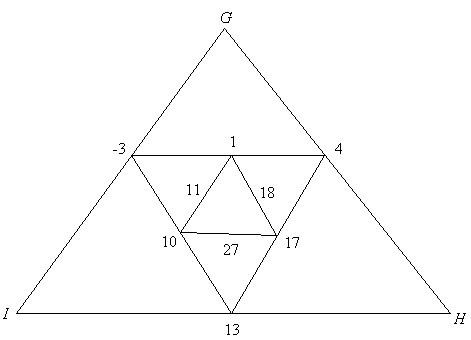
Figure 26: Stacey’s third triangle.
(65) Stacey: Oooh. Let’s keep going.
(66) Kerry: OK. —
(67) Stacey: This is negative 3 — This is 4. And they join each other.
(68) Kerry: You didn’t drop this low enough. Soon you’ll need a huge sheet of paper.
(69) Stacey: OK
(70) Kerry: Pretend the corner’s there.
(71) Stacey: That was 4. And this is —13.
(72) Kerry: OK. G H and I. — So I plus G equals negative 3. G plus H equals 4. H plus I equals.
Here Stacey extends lines again, producing the diagram shown in Figure 26. Kerry immediately begins setting up the equations to solve this new triangle by mechanical deduction (line 72).
6. Inductive reasoning to explore
In this episode Stacey and Kerry explore inductively, and reject conjectures based on short unformulated proving, or verify them inductively. The transcript continues directly from the transcript in episode 5.
(73) Stacey: Do you know what?
(74) Kerry: What?
(75) Stacey: — OK. You want a prediction?
(76) Kerry: OK. Sure.
| (77) Stacey: | Well I don’t know about this. This is just the one little step. This is decreased by 14. This is decreased by 14. And this is decreased by 14. — |
(78) Kerry: What’s that mean?
(79) Stacey: From here to here.
(80) Kerry: I see that. That’s-
(81) Stacey: Yeah
(82) Kerry: -pretty neat.
(83) Stacey: Yeah.
(84) Kerry: Yes.
(85) Stacey: Keep going. Does that mean this will decrease by 14? For this line here?
(86) Kerry: OK. For H. Well.
(87) Stacey: Is that a prediction that H is 3? Go for it.
Stacey’s prediction comes as the result of exploring by inductive reasoning. She has seen that 27–14=13, 18–14=4, and 11–14=–3 in this case. She is aware of the weakness of generalizing from one case “This is just the one little step” and so she urges Kerry to find the solution for the –3-4-13 triangle in order to provide
another case on which to base an inductive argument. Kerry solved his system of equations (again using mechanical deduction to explore towards a specific goal) and soon found that H=10, contradicting Stacey’s conjecture. The rejection of her conjecture at this point qualifies as verifying the falsehood of her conjecture by unformulated proving involving a single deductive step.
After Kerry had found the values of G, H, and I, Stacey and Kerry advanced new predictions. Kerry predicted that the next difference would be 3.5, reasoning inductively that the differences, 14 and 7, were being halved at each stage. Stacey suggested that the differences might alternate: 14,7,14,7,... To test Stacey’s prediction they switched from their previous pattern of solving each new triangle using a system of equations, and instead tried the values predicted by Stacey directly on the new –6-3-10 triangle. When the predicted values failed to work this verified, by way of simple unformulated proving, that Stacey’s prediction was wrong. Stacey observed that her prediction was based on inductive reasoning from very little data, so it was not surprising when it failed. Kerry then returned to his systems of equations to find the correct values. They conformed to his prediction of a decrease of 3.5, verifying his conjecture inductively. To provide further inductive verification, Kerry predicted the values for the next triangle, and tested them. At this stage they both accepted as a general principle that the difference for each triangle was half of the difference for the triangle contained in it.
7. Unformulated proving to explore
Having verified a generalization inductively, Stacey and Kerry were now in a position to explore by proving from their generalization. In episode 7 they did so. In fairly quick succession they made two predictions based on unformulated proving. They predicted that if they drew a triangle inside the original 11-18-27 triangle, the values on its sides could be found by adding 28 (14 times 2) to the values on the 11-18-27 triangle’s vertices. They did so, which provides an example of exploring deductively, followed by verifying inductively, precisely the opposite of the pattern suggested in curriculum documents (e.g., NCTM, 1989) and the research literature (e.g., Fischbein and Kedem, 1982). They then reasoned that there would be a limiting value for the numbers on the triangles if the process of adding triangles outside was continued indefinitely. Aside from a quickly rejected suggestion that Stacey calculate this limit, they made no additional attempt to verify this conjecture, presumable because an inductive verification would have been laborious, and the unformulated proving which suggested it also verified it. This episode ended with Stacey suggesting that they find a formula for their conclusion, but the confusion of variables in their diagram convinced them that this would be difficult.
8. Reasoning by analogy to explain
This episode marks the first time Stacey and Kerry evidenced a serious need to explain. Kerry wondered why the initial difference in their triangles had been 14, and also why his matrices had not produced the correct answer. Stacey experimented with the numbers involved in the original puzzle, and discovered that 56, that is (11+18+27), is evenly divisible by 14. This lead them to conclude (by the same inductive “It can’t just be fluke” reasoning Kerry employed earlier) that the number 4 must be significant in some way. Their interest then turned to explaining
the association of 4 with the original situation. They each noted an analogy which would explain 3 being important, as if they were attempting to find analogies for 4 and failing. Stacey noted that triangles have three sides, which Kerry noted that finding the sum of three numbers and dividing by 3 would be taking the average of them. Kerry even went so far as multiplying 14 by 3 to see if that product would be related to the situation in some way. These associations with 3 are imperfect examples of explaining by analogy, as they fail to explain the occurrence of 4. In episode 10 Stacey offers a more reasonable analogy to explain the occurrence of 4.
9. Inductive reasoning to explore
One of the observers, Tom Kieren, interrupted them at this point, and asked “Is 14 special, or is one fourth of the sum special?” This provoked further inductive explorations directed towards the goal of seeing whether 14, or 4, was a general feature of the Arithmagon situation. The checked one of the triangles they had already produced by extending lines, and a new triangle with sides 8, 19, and 21. These explorations led them to make a new conjecture, of a general method for solving Arithmagons:
(1) Kerry: Hmm? Yeah, OK. — Well, we figured out that’s how it goes, eh?
(2) Stacey: Yeah, it’s quite constant.
| (3) Kerry: | You take the. So if we. If we were first given this, we could’ve — found the sums, right off the bat. We found the sums. Found the sum, sorry, the sum of these three. — Of these: 11 plus 18 plus 27 equals 56. We divided that by 4, right off the bat. We got our 14 to start with. — |
Stacey interrupts Kerry’s description at this point, but to continue and clarify it, their method is as follows. First they extend the diagram by adding a second triangle around the first one. Next they add together the three known sides (“11 plus 18 plus 27 equals 56”), and divide by 4. In this case this gave them 14. Subtracting this result from each of the known sides gives values which they assign to the corners of their outer triangle (see Figure 27). Adding these gives numbers for the sides of the outer triangle, which are also the values for the secret numbers on the corners of the inner triangle.
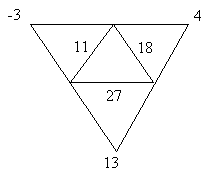
Figure 27: Values on the outer triangles.
10. Reasoning by analogy to explain
Having developed a general method for solving Arithmagons, they then returned to the problem of explaining the importance of the number 4. This transcript continues the transcript in episode 9.
(4) Stacey: But why did we divide by 4?
(5) Kerry: Because 4 is the. We figured out 4 is the magic thing here.
(6) Stacey: Yeah, but why?
| (7) Kerry: | Oh yeah, OK, so we figured it out anyways. — But we now have to figure out, why 4? So we figured out the system, now we’ve just got to understand: why the system? |
(8) Stacey: Yeah.
(9) Kerry: Why is 4-
(10) Stacey: Yeah.
(11) Kerry: So important?
(12) Stacey: A triangle has 3 sides, and 3 points. When you cut that in 1, 2, 3, 4,
(13) Kerry: What? How are you cutting that in 4?
| (14) Stacey: | Why didn’t I just see that? But does that have anything to do with it? Here you have a triangle. There you have a triangle. Here you have a triangle. There you have a triangle. |
(15) Kerry: Well that’s 4 triangles. —
(16) Stacey: We’ll just use that, OK? [laughs]
In lines 10-14 Stacey has finally found something in the problem situation which is associated with the number 4. She observed that the act of nesting the original triangle in a larger triangle created four triangles approximately the same size as the original (see Figure 28).

Figure 28: Stacey’s four triangles.
Kerry was unhappy with this explanation however, “You can’t just say that, you have to explain that. Why are those 4 triangles important?" Stacey’s analogy is a weak one, between the geometry of the situation and the method of its solution, so it is not surprising that neither of them had much faith in it.
11. Further exploring
At this point the problem session ended. Before they left Stacey and Kerry asked if they had done what we had expected; if they had found the answer, as it were. After congratulating them on following a path which we had not anticipated in the least, we commented that investigating Arithmagon squares was one generalization we had thought that some participants might make. Stacey and Kerry reported when they came in for the GEOworld session the next week that they had gone to the library and spent many hours exploring how their method could be extended to Arithmagons of four or more sides, evidencing a strong need to explore at that time.
12. Formulated proving to explain, interpreting a semi-formal proof
When Stacey and Kerry left the Arithmagon problem session, they were still wondering why the number 4 had come up in their general method for solving the Arithmagon . In the interview session, they were shown a formal proof (see Figure 29), which derives a formula equivalent to their solution method from the relations given in the problem. For Kerry this proof explained the need to divide by 4 in their method. Several times he made comments like “That’s where we get the 1/4 from, Neato” and “That’s the 1/4 rule.” For him the formulated proving involved in interpreting the proof satisfied his need to explain.
My claim that formulated proving is involved in the interpretation of proofs is based on my own experiences, and the following analysis by Freudenthal (1973).
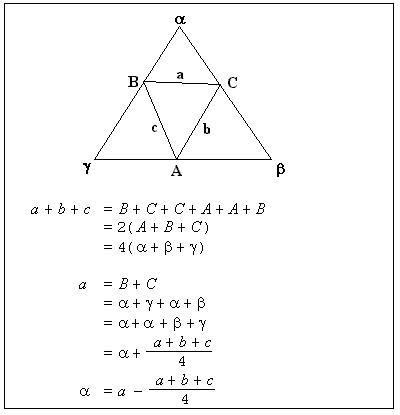
|
Figure 29: The proof shown to Stacey and Kerry in the interview session. |
The only mathematician I can tell precisely of how he reads mathematical papers, am I myself. I never read mathematical papers from the first to the last word. I start with the results. I appreciate them being neatly exhibited. Then I think about them. If I cannot confirm them, I look through the paper for some indication how they can be proved. Maybe I then succeed in confirming the results. Otherwise I look for lemmas I understand and try to derive the main theorems from them. Maybe I have to take a closer look at some proof; if an earlier result is referred to, I go back to it. If finally by my own means and a bit of cribbing I have confirmed the results, that is, if I master all the connections, I am likely to read the papers through once again systematically. Others have told me that they also read papers written by others in approximately the same way. There are people who can read papers systematically, page by page, line by line, letter by letter. To do so testifies to a strong discipline of mind which is not everybody’s attribute. I think it is the rule that in trying to understand papers written by others, people behave as if they are making original investigations. They try to reinvent the contents of the paper; this is a bit easier than brand-new inventions because you can crib as much as you want. (1973, p. 115)
Interpreting proofs involves a process of proving, guided by the proof. This process need not begin with the definitions and premises of the proof. In fact, in the case of many proofs, this approach would be quite difficult. The process of interpretation involves a loose reading of the proof, identifying the basic structure, and looking for aspects which might cause difficulties. Once this is done, tricky parts of the proof might be examined in more detail. It is at these times that the definitions and premises chosen often turn out to be relevant, because they were chosen by the originator of the proof not before proving, but during the process, as the need for them arose.