previous table of contents next
2. Exploring
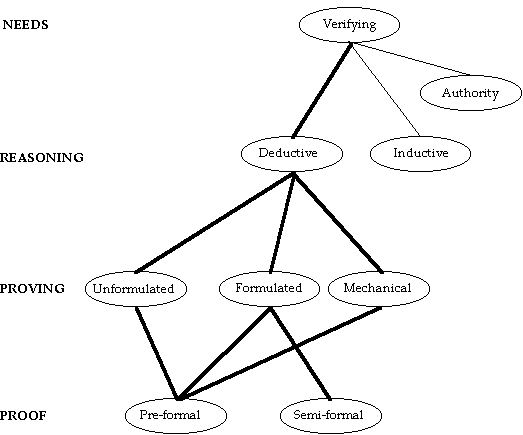
Given the exploratory nature of open ended problem solving it is not surprising that the need to explore arose often in my studies. This need occasioned both unformulated and formulated proving as well as an important kind of proving that I call mechanical deduction. Mechanical deduction involves the use of a technique or technology that is based on deductive principles, but that conceals the operation of these principles in a set of mechanistic rules. Algebraic manipulations are included in mechanical deduction, as is computer programming. Both reasoning by analogy and inductive reasoning were also used to explore, and examples of such reasoning are discussed at the end of this section. Figure 14 shows the paths in the network related to exploring, with paths involving proving marked by thicker lines.
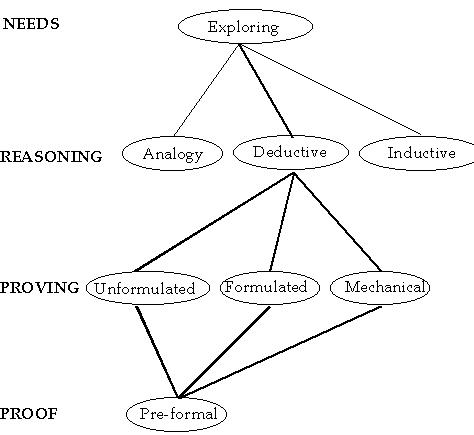
Figure 14: Paths related to exploring.
Exploring — Unformulated proving
Several episodes of unformulated proving used to explore were observed. In each of these it seems that such explorations must be successful quickly or not be successful at all. It seems also that the results of such explorations are not remembered unless they are later formulated. The cases here show a successful short term exploration (the case involving Bill), and a case of unformulated explorations that were remembered because they were later formulated (the case of Sandy, a grade 6 student).
Bill’s unformulated exploration
This case is taken from Bill and John’s investigation of the Fibonacci situation. After they had been working for about 30 minutes, I asked them to summarize their results (MAT episode 11). After listing three of the relations they had discovered, Bill made this claim: “The first number here would have to be 0, because 0 + 1 = 1.” This claim is an example of a simple deduction of a value in the sequence from the recursive rule defining the sequence. Any extension of the sequence, such as determining the value of F9 from the values of F8 and F7, would be logically the same. Bill’s claim is different in that it uses the recursive rule in an unusual way, to extend the sequence backwards beyond its “beginning”. He found that the recursive rule and deductive reasoning allowed him to circumvent the given situation: “the sequence of Fibonacci numbers begins: 1, 1 ...;” and to invent new mathematical objects, in this case F0. It is the novelty of the result obtained that makes this case an example of exploration.
Sandy’s formulation of his unformulated proving to explore
I made several informal visits to meet with Sandy at his school when he was in grade 6. His ability in mathematics was impressive and inspired my visits. On my first visit I asked him to investigate the Arithmagon situation. He solved the original puzzle quickly through unformulated proving. As he solved a second puzzle his reasoning became more formulated and when asked he could produce a formula and provide a proof of it.
When Sandy was first given the 11-18-27 Arithmagon, he guessed 5 as the value at the top corner, but then rejected it without trying. He then adopted a more systematic approach. He tried 0 and mentally determined that it didn’t work because 11 + 18 = 27. He then observed that the choice of the value at the top corner determines the values of the other two which must add up to 27: “That would make these two numbers and then you just have to find one that makes 27.” He also commented: “I knew it was a fairly small number because this [27] is almost these two [11+18] together.” Although he did not say anything at the time, based on his later comments, I believe that when he tried 1 and found that it worked, he also observed that the sum 11+18 contained the top corner number twice and each of the others once. This allowed him to deduce that the value of the top number would be half of the difference between 11+18 and 27, that is, 1.
Sandy was then asked to make up an Arithmagon of his own, and he chose 13-21-42. He added 13+21 mentally and then subtracted 34 from 42. This gave him 8, which he took half of to arrive at a value of 4. These calculations came quickly and confidently, indicating that he had worked out a method similar to that described above while solving the original puzzle. When Sandy checked his answer, however, he discovered a problem. 4 was not the correct value.
He then tried 2 and when it didn’t work he asked: “Are there only certain combinations that work out here?” He was reassured that the puzzle should work, and then realized the value would have to be negative: “The number’s too high — unless you put –4.” He immediately tried –4 and found that it worked.
(1) DR: Why did you go straight to –4?
(2) Sandy: Because these two [13+21] were less than that [42], you need negative numbers.
(3) DR: But how come 4?
(4) Sandy: I subtracted 34, the total of this, from 42, which gave 8 divided in half. ... I tried 4 first, remember?
(5) DR: Yeah.
(6) Sandy: I figured 1’s not enough, 0’s not even enough, so I tried –4.
Here Sandy’s reasoning is much clearer. He took the sum of the two adjacent sides, found the difference from the opposite side, and divided by 2. At first he took the positive difference which gave him 4. When this failed, he briefly turned to a systematic inductive approach, dividing by 2 again and then reasoning about the size of the number he was seeking. When he realized the answer must be negative, he returned to his original method, seeing that it was sound. He then repeated his calculations in an organized way to show that they gave –4.
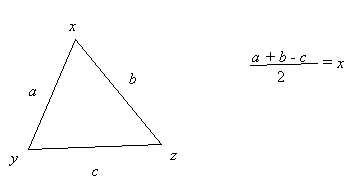
Figure 15: Sandy’s formula for the Arithmagon.
After repeating his calculations for the original puzzle, to show how they worked in that case, he was asked to solve two more Arithmagons and to write his method in formal terms. This he did. He solved a triangle with fractional values as secret numbers without comment and finally produced the diagram and formula in Figure 15.
Sandy’s original proving, which led him to the discovery of his method, was unformulated, but the problems he had with the second puzzle, and the questions he was asked led him to formulate it somewhat. This enabled him to used his method intelligently in cases with fractional solutions and later when exploring Arithmagon squares.
Exploring — Formulated proving — Preformal proof
In all the studies I did as part of this research, exploring using formulated proving occurred in only one case: Rachel and Eleanor’s investigation of the Arithmagon situation with Ben and Wayne. The association of this proving with a need to explore should be qualified by the observation that Rachel’s initial choice to explore by proving was motivated by the expectations she ascribed to one of the observers. Eleanor’s choice to prove as a way of exploring may be linked to her observation of Rachel’s activities.
Rachel’s explorations by formulated proving
For the first half hour of the session, Rachel engaged in activities similar to those of the others. She solved the original puzzle by using a system of equations, she tried solving other triangles, she experimented with Ben’s constraints method, and she searched for patterns inductively. In the second half hour of the session, however, she worked by herself, or with the help of an observer, Tom Kieren, using formulated proving to explore. Her first exploration was of the situation in which two of the known sides are equal. By working with the known relations she was able to deduce that two of the corners would be equal in that case (see Figure 16). After she came to this conclusion, she described her work to the others MAT episode 8). This description may have inspired Eleanor’s explorations by formulated proving (see below).
Rachel then explored the case of all the known sides being equal. When she completed her deductions, the observer closest to her, Tom, suggested that she explore the situation without putting any constraints on the situation. With a few hints from Tom she then derived a general formula, x = -> , for an unknown corner.

Figure 16: Rachel’s proving to explore.
While Rachel’s proving led to her discovery of new aspects of the Arithmagon situation, it would be misleading to claim that exploring was her sole
motivation to prove. Her comments in the interview session make it clear that she had other considerations in mind.
| (1) DR: | Why were you doing that? |
| (2) Rachel: | Oh, you want me to answer right now? [laughter] Because I was stuck at them. I didn’t know where to go. And Tom was sitting beside me saying, “Well, what can you do now?” |
| (3) Eleanor: | Nothing, nothing. [laughter] |
| (4) Rachel: | So I was thinking I’d better think of something, or else that question’s going to keep coming. So I just thought, well hey, in math you always get that right? You always get those conditions. Every teacher’s listing these conditions. Now, if we have this condition where this equals that. You know what I mean. So that’s. It just. You know. It comes from my head. Something I knew of already that I thought I could apply to that problem. |
Here it seems that the form of Rachel’s proving was taken from her past school experience, in the hope of satisfying her need to answer Tom’s question “What can you do now?”
Eleanor’s explorations by formulated proving
While Rachel was exploring the Arithmagon situation modified by various conditions, Eleanor was working with Ben and Wayne. Together they found inductively the relations a+z = b+y = c+x and a+b+c = 2(x+y+z) (see Figure 17). Eleanor then worked independently, trying to invent a general method of solution based on these relations (MAT episodes 11-13). Her work was interrupted on several occasions but she did manage to develop an alternative solution method to Rachel’s. Her method involves finding the sum of the three sides (34, in the example shown in Figure 17), and dividing by 2 (17 in her example, but not shown). This calculation gives her “middle number,” (note the expression in the middle of the upper triangle). Because the sum of a side and the corner opposite is this middle number, the corner numbers are obtained by subtracting across the triangle (e.g., 17–11=6).
Eleanor’s explorations differed from Rachel’s in an important respect. Rachel began from the conditions known to her and those she added, and explored to see what she could find out. She had no particular goal in mind. In Eleanor’s case, she had the specific goal of finding a general solution method. One difference between exploring with a goal and exploring without one is the criteria for satisfaction. In Eleanor’s case, her proving could only satisfy her need to explore if she found a general method. In Rachel’s case, whatever particular results she found satisfied her need to explore. It was only the teacher-game she felt she was playing with Tom that kept her proving (Other teacher-games are described in section 4).
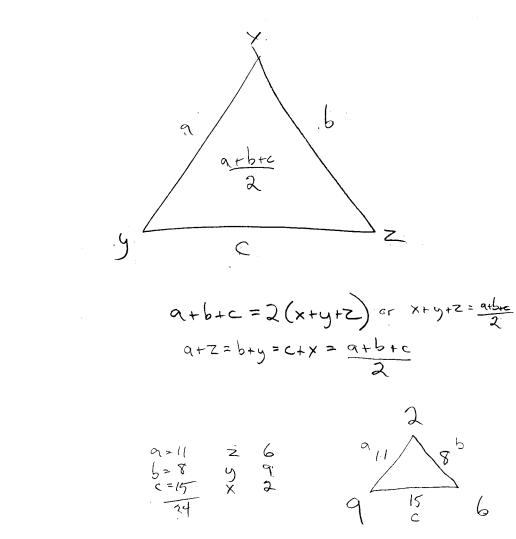
Figure 17: Work related to Eleanor’s formulated proving to explore.
Exploring — Mechanical Deduction — Preformal proof
Particular circumstances are necessary for mechanical deduction to be used to explore. The situation has to be one in which what is known about the situation can easily be cast into a form to which a particular technique is suited. The Arithmagon situation is one such situation. Kerry, Jane, Chris, Rachel, and Eleanor in the first clinical study, and Colin in the North school study, used mechanical deduction to solve the original puzzle (see Chapter III for Stacey and Kerry’s uses of mechanical deduction, and Appendix E for descriptions of ways of solving the Arithmagon puzzle).
When the information given in the problem is cast into an algebraic form a system of three equation in three unknowns is generated:
a + b = 11
b + c = 18
a + c = 27
This system of equations can be solved by elimination, using procedures that were known to all the participants in the studies except Sandy, Bill and John. The system can also be solved as a matrix, and this was done by Kerry and Chris.
Chris’s explorations (his partner, Jane, was not very actively involved) were unusual for the strong preference he had for mechanical deduction. In the Arithmagon situation (see MAT) he solved the original puzzle using a system of equations and felt he had established a general method. I then suggested he try an Arithmagon square. Some Arithmagon squares have an infinite number of solutions, and some have no solution. He began working with a matrix, which he row reduced correctly, as far as was possible. He was not able, however, to give meaning to his result. He continued wondering what was wrong with his matrix for an extended period. At no point did he attempt an example, which might have indicated to him the nature of his difficulties with his matrix. In the Fibonacci situation he formalized the rule as F1=a, F2=b, Fn=Fn-1 + Fn-2. He then derived a wide variety of statements from this rule, without interpreting any of them in terms of the actual sequence. At one point he obtained a sequence of expressions, that included the Fibonacci numbers as coefficients, but he did not notice. The mechanical deduction he was engaged in kept him from seeing any meanings in what he was doing.
That mechanical deduction was not employed for exploration more extensively is probably an indication of the unusual conditions present at the beginning of the investigation of the Arithmagon situation, compared to the conditions later in that situation and generally in the Fibonacci situation. In the Arithmagon situation an algebraic expression of the situation is easily obtained, and is of a form familiar to most of the participants. These problem situations are unusual when compared with the exercises the students at Central, North and South Schools saw in their mathematics classes. In the schools the majority of exercises the students are assigned are set up to provide a fairly easy entry for the algebraic techniques used for mechanical deductions.
For example, at South High School the students were assigned problems asking them to determine, given the coordinates of four points, if those points were the vertices of a parallelogram. In class they were specifically instructed that a careful graph of the points would not suffice to answer the question, even if the graph clearly showed two sides were not parallel. A correct solution to the exercise required that the students employ the slope formula to determine the slopes of the two segments in question. The exercise was set up to make mechanical deduction using the slope formula easy, and the teacher’s instructions required it.
Exploring — Analogy
Many participants in the studies considered whether the triangle in the original Arithmagon puzzle might offer a clue to its solution. Wayne was unusual in that he took this clue seriously, even when told that the situation had nothing to do with triangles. Wayne explored the Arithmagon situation by drawing analogies between the situation, and his knowledge of triangle geometry (MAT episodes 1, 3, 5, 6, & 16). This made triangle properties like area, Pythagorean triples, and angle measure relevant to his exploring (see Figure 18).
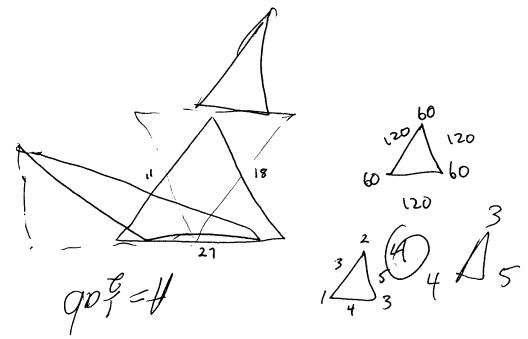
Figure 18: Triangles drawn by Wayne while exploring, relating to geometric properties.
This unusual use of analogy to explore interfered with Wayne’s ability to identify patterns inductively and so interfered with the satisfaction of his need to explore. His lack of success need not have been the case, however. The main limitation of his use of analogy was the weakness of the analogy. Nothing but the arrangement of the puzzle suggested that triangle geometry might be involved. Perhaps if the analogy had been stronger, Wayne might have enjoyed successes like those of Euler, who used analogy extensively in his mathematical explorations (Polya, 1968).
Exploring — Inductive reasoning
Exploring inductively was used extensively by all the participants in the studies. This is not surprising. In many circumstances the information given provided a weak base for both analogy and proving. In addition, inductive exploring was the way of exploring most often modeled in the schools.
Inductive exploring was used more often in the Fibonacci situation than in the Arithmagon situation. This may be due to the ease of generating new data in the Fibonacci situation. In the Arithmagon situation new triangles could be generated by starting with known corner numbers and adding to find the side numbers, but this technique produced Arithmagons with special properties. To generate general examples, new puzzles had to be made, and then solved. Even with the use of mechanical deduction this process was time consuming. Most participants examined only a few Arithmagon triangles. On the other hand, most participants examined from 20 to 40 terms of the Fibonacci sequence. Another feature of the Fibonacci situation, that may have discouraged deductive reasoning, is the recursive formulation of the rule defining the sequence. While unformulated reasoning was not hampered by this feature of the situation, the participants are unlikely to have had much experience reasoning formally on recursive sequences.
In the GEOworld situation the students were asked to try to identify features of a geometric world defined by a computer procedure that drew geometric figures based on three numeric inputs. For example, Figure 19 shows the results of the inputs 100, 100, 3. In this situation the students had no general knowledge of the situation at all. Any general principles had to be developed inductively by them. I was interested to see whether the establishment of such principles would give rise to a need to prove from them, or whether some need to prove would motivate the participants to establish general principles.
Figure 19: Output of GEO 100 100 3.
In the end, the GEO situation provided little information about proving, because almost all the reasoning employed in that situation was inductive. This reflects the complete lack of known relations available at the beginning of the participants’ investigations. In a few cases reasoning by analogy and unformulated proving were used, once some patterns had been established, but these were fleeting.
Summary
Exploring is the need that was satisfied in the widest variety of ways by the participants in my studies. Both inductive reasoning and reasoning by analogy were used to explore, but exploring inductively was far more common and far more successful. The proving used include unformulated and formulated proving and mechanical deduction. The problem situations themselves seemed to be the strongest constraints on the method of exploration. The exception to this is the case of formulated proving, which seems to require a supportive social context to occur.
Unformulated proving can satisfy a need to explore, but only in cases where the situation is not too complex. Simple discoveries like Bill’s occur in isolation
and are unlikely to be connected with other aspects of the situation. Sandy provides an example of unformulated proving which became sufficiently formulated to be used and extended as exploration of the situation continued. As with explaining by unformulated proving, the proving that occurred in these examples is difficult to detect and lacks the permanence that formulated proving seems to possess.
Exploring by formulated proving was an uncommon method of exploring for the participants in the studies. This seems odd considering its usefulness as a method of exploration. It may be that other methods of exploration are just as useful, or that students have more experience with other methods of exploring. Exploring can be directed to a particular goal or undirected. Formulated proving is useful in both cases although satisfaction is likely to come more quickly if no particular goal is sought. Finally, as in the case of explaining by formulated proving, social factors seem to be important in the use of formulated proving to explore.
3. Verifying
|
Figure 20: Paths related to verification. |
Verifying is traditionally and most commonly thought to be the need which proving satisfies. As I noted in the previous chapter, this is not the case in mathematics nor for many students. The participants in my studies did prove to verify, but only in particular circumstances. For example, unformulated proving was an integral part of “guess and check” inductive explorations, forming the “check.” Proving which was begun to satisfy some other need can also verify. All three kinds of proving I identified are include in the network shown in Figure 20 because of this incidental verifying which occurs. Formulated proving to verify also occurred as part of a teacher-game. These occurrences are described and discussed in the next section, which is focused directly on teacher-games as a need to prove.
Inductive reasoning can also be used to verify and an example and discussion of this will also be given. While not a kind of reasoning, appeal to authority can also be an important way of verifying in mathematics, and so I include it as part of the network. Appeal to authority was only observed with the high school students. Figure 20 shows the paths associated with the need to verify. Those involving proving are marked by thick lines.
Verifying — Unformulated proving
Unformulated proving was used in conjunction with inductive exploration in a ‘guess and check’ cycle. While many ‘checks’ were simple calculations, which I do not count as deductions (although technically they are), others were more involved. A particularly clear example is Bill’s verification of a method he found for solving the Arithmagon. Bill had been experimenting with various operations on the three known sides to try to derive a secret number. When he calculated 27 ∏ 18 ¥ 11 ª 16.5 he felt he was near a solution (MAT episode 6). Once he had rounded 16.5 to 17 he could determine the other secret numbers by subtracting from the sums on the sides. Bill had at this point found a solution method that worked for a special case. Now he needed to test it in general. He asked “But would it work for any one?” and tried the case of a 3-6-17 triangle. His method gave him a value of 9, which he felt was wrong.
To verify that 9 did not work Bill used unformulated proving by reducio ad absurdum*. “No, how could it be 9? Because you, you get 6. [9+?=6] Unless this was, um, negative three. [9+(–3)=6. Another secret number must then be –3.] But then you get 3 from here. [(–3)+?=3] You would have to have, um. To get a negative, you have to have 6. [(–3)+6=3. The third secret number would have to be 6.] But then 9 and 6 is 15. [Not 17, as it should be. A contradiction has been reached.] It would not work.”
While most participants were not so clearly using unformulated proving to verify results, this does seem to have been fairly common. This seems reasonable since the main weakness of unformulated proving, the impermanence of the process and result, does not matter in cases where the result will be discarded if found wrong. It should also be noted that unformulated proving to explain or explore can also verify the results involved, and some examples included under those headings could also appear here.
Verifying — Mechanical deduction — Preformal proof
Colin was observed using mechanical deduction to verify statements during the first interview session at North School. There is an interesting contrast between Colin’s use of mechanical deduction and Anton’s use of inductive reasoning to verify.
* Deriving a contradiction.
In the first interview session I asked Colin and Anton to reexamine a calculation they had made in the Arithmagon situation. They did so, and Colin noticed an error in it. This allowed him to perform a correct calculation which produced the formula Z . When I asked Colin what this formula meant, he said with confidence that it gave one of the secret corner numbers. Anton then suggested trying it to see if it worked. They did so. Anton then suggested trying it on a different corner. They did so, and I asked if they had expected the formula to work on one corner but not on all. Colin asserted that the formula should work the same way for all corners (MAT episode 2.5). Anton then asked me if the formula was correct, and I said it was one of several correct formulae. These episodes were followed by Colin’s use of formulated proving to explain, described in section 1.
What distinguishes this case from those of formulated proving described above is the use of mechanical deduction to discover and simultaneously verify the formula. The mechanical aspect of Colin’s derivation was revealed more clearly later in the session when I asked them to interpret the derivation in terms of what it meant to subtract the two equations relating sides to corners. They were unable to do so, indicating that the original subtraction was not a formalized act of deductive reasoning but a mechanical act of deductive reasoning.
Verifying — Inductive reasoning
Verifying using inductive reasoning was observed far more often than verifying by proving. This seems to be the method of choice for verifying in mathematical situation for the participants in the studies. Colin and Anton provide a sharp contrast between these two methods of verifying (described under Verifying—Formulated proving). Such a sharp contrast is not visible in many other cases, since few people verified by proving while everyone verified inductively.
Inductive verification was used often even when a deductive verification could easily have been provided. For example, when Rachel announced her formula for solving Arithmagon puzzles, she made it clear that she had derived it. Ben and Wayne, however, did not ask her how the derivation went, but instead tried her formula on a example and concluded that it worked.
This overwhelming preference for inductive reasoning as a way of verifying has been demonstrated by many studies (e.g., Fischbein & Kedem, 1982) that claim that students do not understand proofs because they prefer to verify statements inductively. The possible implications this could have for teaching proving are discussed in Chapter V.
Verifying — Authority
The way of verifying mathematical statements that was second in popularity to inductive reasoning was a form of non-reasoning: making reference to an authority. Two of the participants at North School, Bill and Anton, provide good examples of verifying by making reference to authority. The participants in the clinical studies seem to have assumed that simply asking for answers was not permitted. They may have been playing a research-game more than a teacher-game. These two high school students, however, were willing to ask, and did so. The
case of Anton gives a simple example of asking for verification. The case of Bill is more complex.
Anton’s reference to authority
Immediately after Colin and Anton solved the Arithmagon puzzle, in the Arithmagon session, Anton asked if their solution was correct (MAT episode 1.4). As they found their solution by means of a mechanical deduction, it is not surprising that Anton might have doubts about their solution. Mistakes happen in mechanical deduction, and are hard to notice. What is surprising is that Anton chose to verify their solution by asking an authority, rather than checking it himself. He seems at this point to have a preference for authority over induction. This was not the general case, however, as Anton verified statements inductively in the other sessions.
Bill’s rejection of analogy, induction, and deduction in the face of authority
In the second interview with Bill and John, we proved that the sum of two odd numbers is even, twice. They both seemed quite confident that this was a general principle. Bill, in particular, had a number of reasons to believe in the generality of this principle. He had seen inductive evidence for it in the Fibonacci session. In the first interview session I had assured him that it is generally true. In both interview sessions he had offered explanations by analogy of the principle. And finally he had just seen two proofs of the principle, one of which he developed himself. When I made the claim, at the end of the second interview session, that the assertion fails for large numbers, their response surprised me. In the face of all the evidence they had seen, Bill and John rejected the generality of the odd+odd=even principle (MAT episode 19).
Both Bill and John’s first response to my assertion that the principle failed for large numbers was to ask “How large are we talking?” I replied that the principle failed for 117 digit numbers. Bill then said: “I don’t see how come that is, but of course I’d have to see a number that long. [laughter] And it would take like a year to really find out why. But, um, That’s really kind of neat.” His comments do not indicate that he couldn’t see how the principle could fail, that he doubted it could, but rather that he could not understand why it would fail. He acted as if the failure of mathematics to make sense in this case was a failure on his part to make sense of it. Against all the inductive, deductive and analogical arguments he had seen, my authority, acting in the role of a teacher, was overwhelming. Neither the possibility that I was lying or mistaken was voiced, and neither possibility seemed even to be considered. (Lest there be concerns about the ethics of my research, I did admit my deception before the session ended.)
Bill’s beliefs about the origins of mathematics may be related to his attitude towards authorities. In line 8 of the transcript in the sub-section Explaining — Formulated proving, in section 1, he refers to “they”, the “brilliant genius” who could develop the formula and then rephrase it in a useful form. Of course, this is exactly what Bill and John did, but Bill quickly removed himself from this creative activity, substituting the anonymous geniuses who create mathematics.
Verifying in school
It seems plausible that Bill and Anton might have developed their attitudes towards verifying by making reference to authority in school. This example from South School illustrates how this might have come about.
Ms. E was teaching a lesson on slopes of perpendicular lines. She had the class suggest relationships between the slopes of perpendicular lines. The first suggestion was that the slopes would be opposites. The example Ms. E had on the board involved slopes of 1 and –1, so in this case the suggested relationship worked. Ms. E then looked an example of a line of slope 3. She drew in a line of slope –3 and noted that the line did not look perpendicular. A student suggested the negative reciprocal. Ms. E. drew in a line of slope , and noted that it did look perpendicular. She then said, “That doesn’t look bad. Again, it’s not a proof, but it’s good inductive reasoning, and in this case it is true.” In this case the students have been given some visual, inductive evidence that the relationship is what Ms. E says it is, but she has then explicitly rejected that evidence as a verification. The students are left to rely on the teacher’s authority as verification.
Summary
Verification, the traditional reason to prove, seems not to be a major motivation for the students I observed. Some unformulated proving and mechanical deduction was used to verify, but either as a side effect of proving for some other reason, or as part of an inductive, guess and check, process. Verifying by induction was quite popular, as one would expect from past research. The popularity of verifying by making reference to authority, especially among the high school students surprised me. I suspect I was being naive. On reflection verifying by making reference to authorities makes a lot of sense.
Verifying by reference to authority is not necessarily a poor method of verification. Matters of historical fact, for example, cannot be verified without consulting and analyzing various texts, which act as authorities. In mathematics verifying by making reference to published proofs saves considerable time and effort, although at some risk, as Wiles found when some of the proofs on which he had based his first proof of Fermat’s Last Theorem turned out to have flaws. The elevation of verification by reference to authority over reasoning as a method of verifying has problems, however. Authorities make errors (or lie as I did with Bill) and reasoning in various ways can discover these errors (as occurred in the case of Wiles’ proof of Fermat’s Last Theorem; see Chapter I, section 2).
4. Teacher-games
Formulated proving, specifically intended to verify, occurred only as a result of an interaction with someone in the role of a teacher. In these cases the need to verify becomes entangled with a teacher-game as a motivation to prove. In addition, proving to verify as part of a teacher game can lead to what I call “formulaic” proof-making. Formulaic proof-making results in a proof, but it is not proving. Instead the proof was constructed according to principles which are associated with the creation of the sorts of proof teachers like. Two of the examples given below illustrate formulated proving as part of a teacher-game. The
third illustrates formulaic proof-making. Figure 21 shows the paths associated with these examples.
Figure 21: Paths related to teacher-games.
Teacher-game/Verifying — Formulated proving
The cases described here come closest to the ‘official’ model of proving of any of the paths I have described. Here the purpose of the proving is to verify, and the proving is formulated. Another characteristic of these cases is that in both of them the proving is occasioned by an observer. By questioning the participants’ confidence a teacher-game is initiated. The first case is taken from the second interview with Colin and Anton at North School. The second case is taken from Kerry’s investigation of the Fibonacci situation.
Colin verifies a particular case by reference to formulated proving
In the second interview session, Colin and Anton determined inductively that n3–n is always a multiple of six. I then guided them through a formulated proving of this statement (described in section 1). After Colin had written out the argument I asked them if they now knew that 4173–417 is a multiple of 6 (MAT episode 7). While Anton checked on a calculator, Colin applied the reasoning he had just written out in general to verify this particular case. He argued that 4173–417 is 416¥417¥418, which includes an even number and a multiple of 3. Colin’s use of formulated proving to verify stands in contrast to Anton’s use of inductive reasoning.
Kerry proves to verify that F3n is even
After spending a few minutes examining cases, Kerry and Stacey determined that F3n is even, inductively. Having solved this puzzle to their satisfaction, they began exploring Fp, the Fibonacci numbers with prime indexes. After about 7 minutes of this they had concluded that Fp is always prime. The observer, Tom Kieren, then asked them about F3n again (MAT episode 4). They looked once more at their table of Fibonacci numbers. Tom then asked, “How sure are you about that?” In response to this Kerry proved the statement in a formulated way, making explicit use of the odd+odd=even and odd+even=odd relations for addition of even and odd numbers:
Kerry: Oh, I’m positive. Because, well, you can see that the- that you’ll add this odd number to an even number to get an odd number. Then you’ll add a- Then you’ll add that odd number to the even number to get an odd number. Then you’ll have two odd numbers to add together to get an even number.
Kerry had already verified his statement inductively, and it seems unlikely he would have produced his clear argument to satisfy some residual doubt he might have had.
Teacher-game/Verifying — Formulaic proof making
Laura discovered the formula for solving the Arithmagon inductively. When I asked her if she was sure her formula worked for all Arithmagons, she replied “Oh, you want me to prove it” and she wrote out the “proof” in Figure 22.
It should be noted that this proof is not correct. Laura shows that if her formula works, then the known relations between the sides and corners will hold. She has proved the converse of her statement. Her proof-making is formulaic, not a result of formulated proving, since she has lost track of the sense of her steps and is ‘going through the motions.’ In a different context she proved differently. When she was shown this proof in the interview session she reported that she had seen a better proof when she got home, and she described a correct proof based on the given relations.
PROOF
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Figure 22: Laura’s “proof.”
Summary
In all of these cases, the use of formulated proving to verify was triggered by an observer’s question. The second interview involved my explicitly guiding Colin and Anton through formulated proving, and I raised the question of the truth of their conclusion in a particular case. Kerry had already verified his statement inductively and it seems unlikely he would have produced his clear argument to satisfy some residual doubt he might have had. Similarly Laura’s “proof” could not have verified her formula for her, as she did not unpack the meaning of her manipulations. I have listed these cases under the heading of “Teacher-game/Verifying” to signal that an important aspect of these episodes is their role as part of a teacher-game, of producing “proofs” to verify a statement for a teacher.
5. Synthesis
This section attempts to summarize what I can now suggest about the need, or needs, to prove displayed by the participants in my studies. The different activities of the participants provide a rich source of possible connections and distinctions between needs, forms, and contexts of proving. I have chosen to summarize the connections that seem most significant to me under the headings of needs. I begin with verification, since it is the traditional purpose ascribed to proving. I then move to explanation, which has been a popular alternate purpose for proving in mathematics education research. Third, I look at exploration, which is important in Lakatos’ (1976) account of professional mathematicians’ reasoning. Finally I consider teacher-games and other social situations.

Figure 23: The complete network.
The relationships between needs, reasoning, proving, and proofs can now be gathered together in a single network. An episode of reasoning connects a need with a way of reasoning and if the reasoning is deductive, the connection continues down through a kind of proving and a type of proof (see Figure 23).
Verification
According to a common understanding of it, proving is about knowing with absolute certainty, verifying without doubt. The participants in my studies,
however, did not use proving to verify except in certain special circumstances. Instead they relied on inductive evidence and authorities to verify their conjectures. This is not unreasonable, considering that in many other fields the accepted form of verification is induction or appeal to an authority. These are also the methods of verification modeled by mathematics teachers, at least at North and South schools. It could be argued that it is precisely the fact that proving is used to verify in mathematics that distinguishes mathematics from other fields and so proving should be taught as the only acceptable method of verifying in mathematics. There is, however, significant evidence raised by quasi-empiricist philosophers of mathematics that it is not the case. They point to contemporary and historical cases that illustrate that professional mathematicians do not verify by proving (see Chapter I, section 2).
It is important to note, however, that the participants in the study did prove to verify in some circumstances. As part of inductive cycles of guessing and checking, unformulated proving was used to test conjectures in specific cases (e.g., Bill in section 3). Unformulated proving is well adapted to this usage. Formulated proving was used to verify by some participants who have learned that proving is the only acceptable form of verification in mathematics (e.g., Kerry and Laura in section 4). While they did not prove to verify for themselves or their colleagues, they did so when an observer asked for verification. It would seem that there are two mathematics going on in these situations: the mathematics of the participant and an ‘official’ mathematics represented by the observer.
Explanation
Proving to explain has been suggested as a good way to introduce proving to students (Hanna, 1989). The participants in my studies did use proving to explain with varying success and accepted deductive explanations. At the same time, explaining by analogy was an unexpectedly successful method of explaining.
The deductive explanations observed in the studies involve unformulated proving, formulated proving producing preformal proofs, and formulated proving to interpret semi-formal proofs. Of these, unformulated proving was not usually successful in explaining to others (e.g., Ben in section 1) although short unformulated proving was used in explanations to the prover (e.g., Kerry in section 1). Formulated proving was more successful as a way of explaining (e.g., Eleanor in section 1). Its main weakness was the time and attention it required of the listener. Semi-formal proofs were also accepted as explanations by some participants but not by all (e.g., Kerry in Chapter III, section 12).
The main rival of proving for explaining was the use of reasoning by analogy. Explaining by analogy was more or less successful, depending on the strength of the analogy. A strong analogy was accepted over a deductive explanation in some cases (e.g., Ben, Wayne, and Rachel in section 1). Some explanations by analogy made connections which could have been established deductively although no participants attempted to transform an analogy in this way.
Exploration
Some exploring by proving was observed but for the most part inductive reasoning was used for exploration. The deductive explorations that were successful were formulated or, in certain conditions, mechanical deductions. Both the problem situation and the social context played a significant role in the choice of deduction for exploration.
Unformulated proving was occasionally used for exploring, but these explorations cannot be counted as successful, since they were forgotten soon after (e.g., Stacey in Chapter III, section 2). Formulated proving was more successful (e.g., Rachel in section 2). The use of proving for exploration required that initial conditions suitable for deduction be clearly accessible to the participants. If these conditions happened to match the requirements of a particular deductive technique, then mechanical deduction was usually used (e.g., solving the Arithmagon using a system of equations). In other cases the proving was formulated and either focused on a particular goal or on reaching novel conclusions. The role of social conditions on proving to explore is discussed in Chapter IV, section 2.
In situations where the participants did not perceive sufficient initial conditions for proving they chose to explore inductively. This occurred in most situations. Exploring by induction was generally successful, occasionally leading to discoveries the observers were not expecting.
Teacher games and other social contexts.
The occurrence of formulated proving whether to verify, explain or explore was usually related to a social context. In the case of verification, the social context was what I call a teacher-game. That is, it was a situation where the perceived expectations of someone in the role of a teacher guide the actions of the prover. There were differences between the social contexts occasioning proving to explore and those which occasioned proving to explain.
The need to explain to others requires that the explanation be in a form that can be understood by others. This encourages formulation of the proving process. The participants’ skills in formulating explanations varied, as did their success in explaining to others. The semi-formal proofs I offered as explanations were also accepted as such by some participants. The interpretation of proofs seems to require similar skills to the formulating of proving, and so formal proofs could not be accepted as explanations by all participants.
Proving to explore occurred both as part of a teacher game and because of the generation of a social context that supported proving to explore. It is this second context that is the most interesting. In Eleanor’s case, at least, the sort of exploring she did depended on the exploring being done by those around her. When working with people exploring inductively, she explored inductively. When working with Rachel, who was proving to explore, Eleanor proved.