previous table of contents next
CHAPTER II
NEEDS AND PROVING
Come, my Celia, let us prove
— Ben Jonson, Volpone, III.v
One object and result of my research into the need to prove is a vocabulary for describing needs, and various ways of proving. The needs suggested in the literature in mathematics education have been described in the previous chapter. They included: verification, explanation, exploration, systematization, communication, aesthetics, personal self-realization, developing logical thinking, and “teacher-games.” Not all of these needs seemed to be felt by the students involved in my studies. In this chapter I introduce the needs I did identify in my studies: explaining, exploring, verifying, and teacher-games. After a short introduction each of these needs will be illustrated with examples drawn from the studies, which show the various ways in which proving and other kinds of reasoning were used to satisfy these needs.
Exploration extends the bounds of what is known. Questions such as “How can I find the measure of this angle? and “I wonder what happens if I add the sides” indicate a need to explore. In the case of the first question it is a need to explore with a goal in mind. In the case of the second question the exploration does not have a goal. De Villiers (1990) suggests that the need to explore motivates proving.
The following example of exploring is taken from the work done by two university students, Stacey and Kerry, while investigating the Arithmagon situation. It is episode 2 in the mathematical activity trace in Appendix C* and also appears as part of the case study in Chapter III. Stacey and Kerry solved the original puzzle by reducing a system of equations. In this episode Stacey explores the situation further.
(1) Stacey: What happens if you add the middle numbers together? —
(2) Kerry: Well I guess we could, hmm.
(3) Stacey: I just want to try something. If you take 27, 18, and 11. 2, 4, 5, 56. Right?
(4) Kerry: Sure.
| (5) Stacey: | And you have — So you add each of those twice, right? — Yeah you do. That’s not going to help you either. That’s what you end up doing right? |
* Mathematical activity traces are summaries of the activities of the participants in a session. They were created for some of the problem sessions and interviews as part of the analysis of the studies. They also provide a context for the episodes I will be referring to, and I will make reference to them when describing episodes for which a MAT exists. Appendix C is divided into two sections. The first included MATs for the students from North school. The second includes MATs for the university students. Within these sections the MATs are grouped according to which pair of students was involved. The Table of Contents lists the exact page number for each MAT in Appendix C
(6) Kerry: What’d you do?
(7) Stacey: You add A, B, C. Then you multiply them by 2. You get this answer. —
As I reconstruct them, Stacey’s thoughts ran as follows: “What happens if you add the middle numbers together? 27+18+11 is 56. And how is that related to the numbers on the corners? Each corner number is added into two of the middle numbers, so in the total of the middle numbers you add each corner number twice. Therefore the sum of the middle numbers is two times the sum of the corner numbers. But just knowing the sum of the corner numbers doesn’t help us figure them out.”
Stacey’s initial comment “What happens if you add the middle numbers together?” indicates an exploratory frame of mind, as does her making observations without a particular goal. That she was not expecting the conclusion she reached is indicated by her dissatisfaction with it: “That’s not going to help you either.”
Verifying involves the determination of the truth or falsity of a statement whose truth value is in doubt. A question like “Is the sum of the sides always even?” indicates a need to verify. Many researchers, including Bell (1976) have identified verifying as a source of a need to prove.
The following example continues from the transcript of Stacey and Kerry investigating the Arithmagon situation, given above.
(8) Kerry: Do you add?
(9) Stacey: 22, and 34. Yup. Do you know what I mean?
| (10) Kerry: | Sorry. So you add this and multiply by 2 so, like, the sum of this is 28 times 2. And it’s 56. Good one. What’s that mean? |
(11) Stacey: Nothing. [laughing]
(12) Kerry: Is that-
(13) Stacey: That was just-
(14) Kerry: Is that true for all of them?
(15) Stacey: Yeah.
(16) Kerry: I guess so. It must be. It can’t just be fluke.
When Kerry asked, “Is that true for all of them?” Stacey could respond that it was, because the exploring she had done also verified that the relationship is generally true for Arithmagons. As Kerry did not see how Stacey had arrived at her conclusion, his verification of it was based on the low probability of such a relationship occurring by chance in this case. Both of them verified, but in different ways.
Explaining provides connections between what is known in a way that clarifies why a statement is true. A question like “Why is the sum of the sides always even?” expresses a need to explain. Bell (1976) and de Villiers (1990) suggest explaining as a need to prove.
The following example, taken from a lesson observed at Central High School, illustrates explaining in a mathematical context.
The teacher, Mr. C, presented his grade 12 class with the
problem of showing that
. He asked, “Can someone
explain why the number of ways of selecting 3 from 8 is the same as 
and the number of ways they could
be chosen to include Mr. C is
. As the total number of ways of
choosing three people from a group of eight is known to be
the equality
is explained by this argument.
The need to explain provided the motivation for the proving Mr. C did for his class. This is indicated by his question “Can someone explain why...”, and by his role as a teacher with a responsibility to explain. The possibility that verifying might have been a motivation is unlikely, considering that verification of this particular sum could have been achieved much more quickly using arithmetic techniques.
A teacher-game is a situation in which students act in a particular way in order to satisfy the implicit or explicit demands of a teacher. Playing a teacher game can be based on attempting to achieve a high grade, or simply facilitating the smooth running of the class, to avoid social discomfort. Alibert (1988) and Schoenfeld (1983) point to the importance in schools of conforming to the expectations of the teacher, playing a ‘teacher-game’, as a motivation to engage in proving.
As an example consider the continuation of the lesson
taught by Mr. C. After explaining
that
Mr. C assigned the students the
task of proving algebraically
. As they were proving I asked
several students why they were doing so.
Six of the seven students I asked indicated they were proving only
because it was an assigned task (the seventh said it was for fun).
In this example it was a teacher-game
that created the need to prove. Other
possible needs had been satisfied by Mr. C’s explanation and authority as a
teacher.
Figure 4: First rank of the proving network.
These four needs form the first rank of a network of paths relating aspects of proving (see Figure 4). As each of these needs is discussed, the relevant part of the network will be expanded. Section 1 elaborates and gives examples of proving to explain, and of the use of reasoning by analogy to explain. A distinction is made between proving that is unformulated, of which the prover is unaware, and formulated proving. Section 2 concerns exploring, and the use of proving,
inductive reasoning, and reasoning by analogy to explore. Proving by mechanical deduction, using a deductive tool like algebra, is described in this section. Section 3 includes examples and explanations of the use of proving and inductive reasoning to verify. Section 4 describes proving that takes place as part of a teacher-game. The chapter concludes with a summary of needs and the proving associated with them.
1. Explaining
|
Figure 5: Paths related to explaining. |
Explaining provided a definite need to prove for the participants in my studies, but proving was not the only sort of reasoning motivated by a need to explain. Reasoning by analogy was also used to explain and was preferred to proving in some cases. In addition, I observed significant differences in the formulation of their proving. In Figure 5 the paths involving explaining in the network are shown. Those involving proving are shown by thick lines. The three remaining stages of the network appear for the first time in this figure. The second stage includes different types of reasoning. The third distinguishes proving by the degree of formulation involved in it. The fourth stage differentiates between proofs, on the basis of the formality of their presentation. In the following examples and discussion of these paths the distinction between “formulated” and “unformulated” proving will be clarified. Pre-formal proofs, described above in Chapter I, section 1, will be elaborated upon, and illustrated with examples. At the end of this section examples of explaining by analogy will be discussed and contrasted with explaining by proving. In the following section the network will be extended, as new nodes in each stage are discussed.
Explaining — Formulated proving — Preformal proof
Perhaps the most important distinction suggested by my research is that between formulated and unformulated proving. Formulation refers to the provers’ knowledge or awareness that they are proving. It could also be described as the degree to which the proving is thought-of and thought-out. Formulation is related to two other characteristics of proving: its articulation and the hidden assumptions made while proving. Articulation and hidden assumptions provide valuable clues to formulation, in addition to being important characteristics of proving in and of themselves.
The extent and clarity of the spoken or written articulation of proving has implications for the possibility of the proving being interpreted by others and for the formulation of the proving. Being aware of one’s own proving and being able to articulate that proving are interrelated. Articulating proving assists in formulating since articulation makes aspects of proving tangible. At the same time, formulated proving is more easily articulated.
All proving involves some hidden assumptions. These assumptions can range from wrong assumptions through implausible and plausible assumptions to assumptions that are known within a community. The formulation of proving reveals hidden assumptions, making the presence of wrong or implausible assumptions less likely.
Explaining using formulated proving can be quite successful; however, it seems to require a suitable social context. Rachel and Eleanor, two undergraduate students, provide an example of the use of formulated proving to explain. Their case, and those of Ben (an undergraduate student), Colin and Anton (two grade 12 students), and Bill (a grade 10 student), illustrate the different social contexts in which formulated proving to explain seems to occur.
Rachel and Eleanor explain the formulae found in the Arithmagon situation
Rachel and Eleanor developed two different methods for
solving the Arithmagon. Rachel
derived the formula
algebraically from the relations
between the three known values, a, b, and c.
Eleanor’s method was based on two observations: that the sum of each
side and the corner opposite it is a constant for a given triangle, and that
the sum of the corners is half the sum of the sides, and is the same constant.
Her method was to find the sum of the sides, divide by 2, and subtract
the side opposite the corner she wished to discover.
At the end of the session (MAT episodes E22, R14 ) Eleanor
and Rachel began to wonder why the relations Eleanor’s method is based on
work, and how their two methods are connected.
They derived the relation a
+
b + c
= 2(x + y + z) independently (see
Figure 6 for the diagrams corresponding to Eleanor and Rachel’s equations).
Eleanor derived it from the given relations between the sides a,
b, and c and the unknown
corners. Rachel derived it from
her formula
(see Figures 7 and 8).
Figure 6: Diagrams corresponding to Rachel’s (left) and Eleanor’s (right) equations.
x + y = a
y + z = c
x + z = b
2x + 2y + 2z = a + b + c
2(x + y + z) = a + b + c
y + b = y + (x + z ) = 1/2(a+b+c)
Figure 7: Eleanor’s proving to explain her method.
Eleanor then asked: “How come this plus this — adds up to the sum of all these?” In other words, why is it that the relation (y + b = y+ x + z), which relates the sum of a side with the corner opposite to it to the sum of the sides, holds? She quickly derived it from the relation b = x + z. Meanwhile, Rachel derived her formula from a formulation of Eleanor’s method.
Figure 8: Rachel’s proving to explain her method.
Eleanor and Rachel did not begin suddenly to engage in formulated proving. Rachel had begun early in the session, as a way of exploring (see section 2). Eleanor had been working with either Ben and Wayne, with whom she worked inductively, or Rachel, with whom she engaged in formulated proving. Eleanor’s sensitivity to the reasoning of those with whom she was communicating illustrates one characteristic of a social context for formulated proving. If others are communicating by way of formulated proving, then this activity might be picked up. This point is elaborated further in section 2.
Ben’s formulated proving to explain to others
When Rachel, Eleanor, Ben, and Wayne investigated the Arithmagon situation, the first person to solve the original puzzle was Ben. When Eleanor asked how he found the solution so quickly his first response was “Don’t ask me that! I don’t know. I just saw it right away.” A short while later, he attempted to explain his method, which he seems to have reconstructed deductively (MAT episode 7). Unlike his attempt to explain using unformulated proving (described below), this attempt was formulated, and much more successful as an explanation.
(1) Eleanor: But you saw that right away.
(2) Ben: Yeah.
(3) Eleanor: Why don’t you try another one and see if -
| (4) Ben: | It’d have to be do-able though — I don’t know. I kind of looked at 27. I don’t know what I did actually. No idea how I got that. — Well I knew, well OK, I kind of knew how I did it. The number, the number between. You know how I did that? The number here [C] had to be less than 27, and less, it had to be less than 18, the number here, right, — had to be less than 18. And the number here [B] had to be less than 11,— right? |
(5) Wayne: Yeah, otherwise they’d add to more than 27
| (6) Ben: | So then the number here [A] had to be less than 18 and less than 11. So, I mean, I just said — This 27 right and this 18 since this number is being added, right, that’s one of the adding factors. |
(7) Eleanor: You mean that this number here?
| (8) Ben: | Well no, I don’t know what I looked at first, but I looked at, I noticed that, it [C] has to be lower than 27 and 18, to be added to each other, right? |
(9) Eleanor: Yeah
| (10) Ben: | And I noticed that 11 and 18 had to be a number less than 11 and 18. And I noticed that it had, the third number, 10, had to be less than 11 and 27. |
Figure 9: Labeling of Arithmagon for description of Ben’s explanation.
In line 4 Ben observes that C must be less than both 27 and 18 (see Figure 9 for labeling of corners). This is true only if the secret numbers are assumed to be whole numbers. Both Ben and the others seem to have made this assumption at first. He goes on in lines 4 and 6 to specify the constraints on A and B. In line 5
Wayne explicitly gives the reason for the constraints. Ben repeats this reason in line 8.
All of the things Ben noticed “had to be” involve making deductions from an assumption that the solution is limited to whole numbers. This allows limits to be placed on the potential values of the unknowns. Once he had completed his explanation, Eleanor showed she had understood it by attempting to use his method to solve another puzzle.
In the previous two cases it was the questions of other participants that provided the social context for the use of formulated proving to explain. In the next three cases it is the interviewer who sets up the occasion for proving to explain.
Colin and Anton explain the origin of their Arithmagon formula
Colin and Anton were two grade 12 students in an academic stream mathematics course. After two problem sessions, in which they worked on the Arithmagon and the Fibonacci situations I interviewed them twice. In the first interview session, after Colin and Anton had derived and verified their formula for the Arithmagon, I asked them why their formula works (MAT episode 3). While Anton referred to the examples they had tested it with, Colin proposed “proving” it:
(1) Anton: This is the relationship between the corners and their sides.
(2) Colin: Right, but how come that works? — They have to be related because-
(3) Anton: Because 11
(4) Colin: Yeah. The one number, defines them both. In this corner.
(5) DR: How do you mean it defines them?
| (6) Colin: | Well, See, if this was 3 and 13, whatever this number [Y] is, is going to affect both of these numbers. [See Figure 10] |
(7) DR: Okay
(8) Colin: So.
| (9) Anton: | ‘Cause if this is 10 more, then this has to be 10 more, in order to get the same numbers, you know. So we have this main point right here. So, if this is more, more, this has to be 10 more, in order to get, |
| (10) Colin: | ‘Cause this number will be the same. So it could be 12, and still this would be 10 apart. So that’s why those two are 10 apart, and that’s where we got this first formula. And then this one- |
After Anton identified one of their equations as the difference relation they had found (Z – X = x – z, line 1), Colin asked why it worked (line 2). They then made the connection with the common corner Y , which in this case is 11 (lines 3-4), which requires that any difference in the sides ((13+Y) – (3+Y)) be due to the difference between the other two corners (13–3) (lines 9-10).
After explaining the relation generally, “The one number, defines them both,” Colin repeated the explanation using specific values. This use of general numbers in proving is less formulated than his general explanation but has greater explanatory power. The use of numbers makes his explanation clearer. He might
instead have rephrased his general explanation into something like “Each side is the sum of this corner number and another number, any difference must come from the other number, as this number is shared by both sums.” In conversation, because of its rapid pace, it is more important that an explanation come quickly and clearly than that it be perfectly formulated. This seems to have been behind Colin’s switch from a general statement to the use of general numbers. Anton’s less formulated way of expressing himself may also have had some influence.
Figure 10: Labeling of triangles for description of Colin and Anton’s explanation.
Colin and Anton’s formulated explanation that n3 – n is a multiple of 6
In the second interview, Colin and Anton were guided through a formulated proving that n3 – n is a multiple of 6. They made this conjecture after examining a number of specific values for the expression. I began by asking them if they would prefer to explore, explain, or verify this conjecture. They indicated that they were more concerned with explaining it. By asking guiding questions, like “What do you know about (n–1)(n)(n+1)?” I guided them through a deductive argument. After we had completed the derivation verbally, I asked if it explained their conjecture. They said it did. I then asked them to write out the argument, and Colin did so (see Figure 11, MAT episode 6). Colin omits the last step of stating that the product of an even number and a multiple of 3 must be a multiple of 6.
Colin’s argument, and the verbal argument that preceded it, occurred in a particular social context, that of a teacher guiding students through an argument. This context encouraged the reasoning to remain formulated and deductive. An interesting aspect of this particular case is that when I asked Colin and Anton if they had discovered anything through the reasoning used to explain their conjecture they said no even though they had remarked on the discovery that n3 –n is the product of three consecutive numbers, with n as the middle number. In this case, the need to explain seems to have kept Colin and Anton from seeing that a need to explore could also be addressed by the same reasoning. One need to prove might interfere with the satisfaction of another.
n3 - n
n (n+1) (n-1) ———
means multiplying 3 consecutive #’s
One of the 3 #’s must be even, another must be a multiple of 3.
Even because when you choose 3 consecutive #’s 1 must be even.
odd, even, odd ( 7, 8,
9 )
even, odd, even ( 4, 5, 6 )
Multiple of 3 because when choosing 3 consecutive #’s one is divisible
by 3.
if n = 3x then
if n = 3x-2 then n-1 = 3x-3 which is a multiple
if n = 3x-1 then n+1 = 3x
Figure 11: Colin’s written proof from the second interview.
Bill and John’s explanations by formulated proving
Bill and John were two grade 10 students at North School. In their first interview session they were guided through the derivation of a formula to solve Arithmagons. Bill followed this derivation, but John had trouble with it. In the derivation of the formula A, B, and C were used to represent the unknown corner numbers. The formula at which we arrived was. It is fairly easy to show that this formula simplifies to C, by rearranging the terms: . Bill used this simplification to show the equivalence twice. John suggested that the formula should be rewritten using variables to stand for the known numbers on the sides: D, E, and F. His formula was: . Figure 12 shows the labeling they used. In the following transcript they compare the two formulae (MAT episode 14).
(1) John: Plus B plus C, which would be F. So in other words, E minus D plus F.
(2) Bill: Yeah. That’s an easy way to think of it.
| (3) John: | So, 63. So we just look. We know E is 63. D is 18. And F is 3. So it’ll make it much easier to work with. I guess. |
(4) Bill: Yeah.
(5) John: Then we can just go from there. We know that’s divided by 2. So.
| (6) Bill: | But, You, you are aware of why it is divided by 2, right? The ... reason this, this would make it kind of easier is ‘cause you would know how much is left behind. You would see that the A’s cancel each other out. The B cancels each other out. You would know that |
you would have 2C. With this you wouldn’t really know that you had to divide it by 2. With this you would.
(7) John: That’s true. — OK. So then would it be
| (8) Bill: | But, uh. Once ... you already knew that you had to divide by 2, some brilliant genius ... could go like E take way D plus F and then have it divided by 2 and that would be the whole formula. That’s how they would word it. From the start. But they won’t know why it works. But they would know it does. This shows why it works. That’s, that’s all I can say. But yeah, yours is pretty good. |
(9) John: OK. So it just works. This is why it works.
(10) Bill: Yeah.
Figure 12: Labeling used by Bill and John for their formulae.
The contrast they make is between John’s “much easier to work with” formula, and Bill’s, which “shows why it works.” Bill’s formula makes it simple to prove that the calculation must end with the division by 2. This association with the formulated proving Bill had done makes it more explanatory. Bill acknowledges that John’s formula is easier to use, but he feels that given that formula, “they won’t know why it works.” This case is similar to the previous case involving Colin and Anton, in that the guided, formulated proving the students engaged in satisfied a need to explain. The need to explain by itself was not enough to motivate the proving, but the addition of a social context that encouraged it occasioned activity that satisfied that need to explain.
In my second interview with them I guided Bill and John through two attempts to prove that the sum of two odd numbers is even. The second attempt was fairly successful, and after they had proven even+even=even and even+odd=odd with my guidance, they were able to prove odd+odd=even independently. After this proving concluded, I asked them if the proof explained why the sum of two odd numbers is even (MAT episode 18).
| (1) Bill: | Um. Yeah. It does explain it, ‘cause, ... this would be the same as, ... an even plus an even. ... In the end result, which were given, even, ‘cause we found that out here, already. ... This is an even plus an odd, which gives you an odd ‘cause, well we found that out. ... ‘Cause it’s plus 1. |
| (2) DR: | Umhmm. |
| (3) Bill: | It’s an even number plus 1 that’s why it’s an odd. Um, yeah. That explains it. |
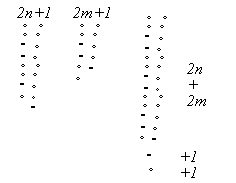
Figure 13: Representation of addition of odd numbers used in Bill’s proving.
Here Bill is summarizing the formulated proving they had done. They represented an odd number both as a column of pairs of dots, with a single dot added, and with the expressions 2n + 1 and 2m + 1 (see Figure 13). In line 1 he is saying that 2n + 2m is even because it is “an even plus an even” which they know is even “ ‘cause we found that out here, already.” That even number (2n+2m) plus 1 “is an even plus an odd, which gives you an odd “ ‘cause, well we found that out.” Bill’s summary is a bit different from what they actually did since in their original proving they considered (2n+2m) + 2, which is even, according to they rule they proved earlier. His addition of 1 may have been a step in a derivation involving the principle that one more than a odd number is even, or he may have been making connections with both of the rules they knew as part of an effort to systematize their knowledge. In any case, I interrupted his summary at this point. What is clear is that he considered their formulated proving to be an explanation of the odd+odd=even rule.
Explaining—Unformulated Proving
As an explanation for others, unformulated proving is inadequate. The lack of articulation and hidden assumptions that come with unformulated proving prevents other people from being able to understand it. For an individual, however, unformulated proving can be used to provide a personal explanation. This is successful when the deductive chain is not too long. Of the cases that follow, Kerry’s concerns a short, unformulated, deduction that explained. Other such episodes probably occurred in the studies, but the very fact that they are short and involve unformulated proving makes it difficult to be sure of their nature, and especially to be sure that they involve a need to explain. The other two cases of explaining using unformulated proving described here illustrate how such attempts can fail when the deductive chain is too long. The first involves Ben, an undergraduate student. The second involves Bill, a grade 10 student.
Kerry’s short explanation
When working in the Fibonacci situation Kerry noticed a pattern in the sums of sequences of three consecutive Fibonacci numbers (MAT episode 6, see Appendix C). He noted that the sum was always twice the last number. For example, he saw that 55+89+144=288. He wondered to himself why this should be so and quickly observed that as the rule defining the Fibonacci sequence told him that 55+89 would be the next Fibonacci number, 144, the sum of three consecutive Fibonacci numbers would always be the same as adding the last of the three to itself.
Kerry’s explaining here is barely articulated, but his assumptions and reasoning are fairly clear. The brevity of his proving contributes to its lack of formulation. A quick deduction like this one does not require any formulation to be continued. Longer chains of deduction become increasingly difficult without formulation.
Ben’s unformulated explaining to others
A group of four undergraduate students, Wayne, Ben, Eleanor, and Rachel, worked together in the Arithmagon situation. Rachel and Eleanor solved the initial puzzle using systems of equations. Ben gave the correct answer almost immediately, and later reconstructed a solution method based on selective guessing guided by the given numbers. At the time this transcript begins (MAT episode 8), I offered him a challenge. My description of the 1-4-12 triangle as “simple” is ironic, as I chose it precisely because the solution includes negative numbers and fractions.
(1) DR: Here’s a simple one: Can you do 1, 4, 12?
(2) Ben: 1, 4, 12, like that?
(3) DR: Well, they’re on the sides, because you’re supposed to be figuring out -
| (4) Ben: | On the sides, 1, 4, 12. Well that’s 0 or 1. One of them has to be 0 — No, That’s impossible — Because, I mean if this one is 0, that one has to be 1, that one has to be 3, this is adds up to 3. If this one is 0, this one has to be 4 and that one has to be 1. |
(5) Wayne: Who said it’s got to be 0 though?
| (6) Ben: | Well, Yeah — It still shouldn’t matter — if you go down on the number line you still have to go up on the number line |
***
(7) Eleanor: 4 and a negative 3
(8) Wayne: Umhmm
(9) Ben: The difference is still a 1 —
(10) Eleanor: but this doesn’t have to be 0
| (11) Ben: | But even if it is, like let’s say negative 4 and negative 3, right? You still have to get this to be 4 it has to be 7, all right? It’s still minus. So it will still be like, 3. — You know where I’m coming from? |
(12) Eleanor: Say it again
| (13) Ben: | The difference, the difference between these two is still always going to be 1, right? No matter if you represent it with negative or adding. |
Ben’s first explanation (line 4), is a fairly well formulated deduction from the principles he had been using to solve other puzzles. He explains why the triangle is impossible by reasoning deductively from the implicit assumption that the secret numbers are natural numbers. When Wayne questions his hidden assumption, Ben immediately offers further explanation (line 6). Note that this explanation has a different character from the ones he has offered before (in line 4). It is much less articulated, making it difficult to judge how aware Ben was of his reasoning. His language suggests that his proving is based on an image of the
relationship between the values. These features lead me to characterize this explanation as unformulated proving.
Eleanor’s request to “say it again” (in line 12) marks the failure of Ben’s unformulated proving to explain to her. Ben has based his argument (in line 11) on a hidden assumption, which in this case is wrong. He seems to believe that the difference between the two secret numbers is 1. This is true in the case where one of them is zero, which he had just been considering. The two numbers he names, –4 and –3, have a difference of 1, and these numbers do not work. In fact, if the difference must be 1, there is no way that a difference as large as (12–4) could occur. This provides the basis for Ben’s belief that the puzzle can not be solved.
Bill’s unformulated explanation that F3n is even
When investigating the Fibonacci situation, Bill and John identified the recursive rule defining the sequence, and found patterns in F3n and F4n inductively. The pattern they saw for F3n was that all such Fibonacci numbers are even. John accepted that this was generally true, based on inductive evidence, although Bill did not. Bill was unusually resistant to accepting inductive verifications. At the end of the session I asked Bill if he could see any reason why every third Fibonacci number is even (MAT episode 16.2).
| (1) Bill: | Um. Why? Um. When you add two odd numbers it goes into an even. That’s one theory. I don’t know. If you. If you add two odds you’d get an even, wouldn’t you? |
(2) DR: Yeah.
(3) Bill: So, let me see. It starts with, uh, with uh one. One, one plus one gives you two.
(4) DR: Umhmm.
| (5) Bill: | And then this it would give you an odd. And then since, uh, then that’s. Oh, wait wait wait wait wait wait. — What was I seeing? [laughs] — —Every third, third number. Oh yeah, Oh no. I’m thinking, right. To get the third number you would add the two odds. Since this is the third number, this would be the next third, third number. There’s two odds, you get an even. This is the third number. There’s two odds, you get an even. |
(6) DR: Would it work- It wouldn’t work if there wasn’t two odds?
(7) Bill: It wouldn’t work if there wasn’t two odds. But since there’s two odds—you can make an even. —
Bill identified part of the deductive argument that shows that every third Fibonacci number is even. The argument involves three steps. The first is to observe that every third Fibonacci number is even because it is preceded by two odd numbers. The second step is to see that this odd-odd-even pattern must recur since it forces the two numbers after an even Fibonacci number to be odd. The final step is to generalize this recurring pattern to the entire sequence. Bill saw the first step, and in line 5 he may have briefly seen the second step. Then he became confused, and soon after he reverted to inductive reasoning to establish that there is always a pair of odd numbers before F3n .
Explaining—Analogy
Reasoning by analogy to explain occurred only a few times in the studies, but those occasions indicated that analogy can be a powerful method of explaining in mathematical situations. The analogies the participants offered can be described as ‘weak’ or ‘strong’ analogies. Their acceptance as explanations was related to this strength. The two cases I will describe in detail involve Bill, and Rachel, Ben, and Wayne. In Bill’s case his analogy is very strong. Rachel, Ben and Wayne each offered explanations of which Rachel’s was deductive, Ben’s was a strong analogy, and Wayne’s was a weak analogy.
Bill’s explanation by analogy
In my second interview with Bill and John, the grade 10 students at North High School, we examined a question that had come up in the first interview session: “Why is the sum of two odd numbers even?”
When the question was first asked (MAT episode 9) Bill gave an explanation by analogy, that he had hinted at in the first interview session. His analogy relates even and odd numbers to positive and negative integers. The rule ‘An odd number plus an odd number is an even number’ corresponds to the rule ‘A negative number times a negative number is a positive number.’ The sums of even numbers and odd numbers are related in a similar way to products of integers.
This analogy is actually quite strong. The integers can be divided in half in various ways, two of which are the division into even and odd, and the division into positive and negative. In both cases there are ethical connotations attached to the words used to describe the two halves, which makes one half “better” than the other. For example, both ‘even’ (as in ‘even-handed’) and ‘positive’ have good connotations. As well, in both cases there is a binary operation that combines two like numbers into a number in the “better” half, and that combines two unlike numbers into a number in the other half. All of these features mark links between the two domains of the analogy. The number of links, and the degree of match between the features they link, is a measure of the strength of the analogy. I am not asserting that Bill would have been able to explicate these links himself, only that they contribute to the strength of his analogy.
After Bill offered his analogy, I led Bill and John through a deductive exploration of the question, using a syncopated algebra to deduce the rules. This was accepted, but not with enthusiasm. I then proposed a pictorial model of the sum of two even numbers and a formal notation related to it. In this context Bill and John were able to prove the odd+even=odd principle with some assistance, and the odd+odd=even principle independently. I then asked Bill and John if what they had done explained the principle odd+odd=even. Bill said it did, and repeated the gist of the argument in order to illustrate how it explained the principle.
About ten minutes later Bill made an interesting comment (MAT episode 20.3). He stated that he did not like proofs, and that he had no interest in explanations of mathematical principles. This statement contradicts comments he made in the first interview session, in which he expressed a preference for his Arithmagon formula and derivation on the basis that they allowed him to see why the division by 2 was needed. This change of heart may reflect the differing circumstances in the two situations. In the first interview session, the proving through which I guided Bill explained his new formula, which was otherwise
unexplained. In the second interview, the statements they proved were already known and accepted, and Bill had already offered his analogy as an explanation for them. If Bill judged his analogy to be a better explanation than the proof, then the proving in this case could be seen as superfluous. As his analogy is a strong one, and he showed enthusiasm for it, I suggest that he did choose it over the deductive explanation offered by the proof.
A strong analogy can indicate the possibility of a deductive link although in the case of Bill this is not so. In the following case of Rachel, Ben and Wayne an analogy that does indicate a deductive link will be described and strong and weak analogies will be contrasted.
Rachel, Ben and Wayne attempt to explain “Why 2?”
The following episode (MAT episodes B19.3, W17.3, E18, R12.1) took place toward the end of a problem session in the first clinical study, in which four undergraduates (Ben, Wayne, Eleanor and Rachel) were working in the Arithmagon situation. It shows both strong and weak analogies, and explaining by proving. Rachel had discovered a formula for determining the value at a vertex x. It is:
where a, b, and c are the values on the sides of the triangle, with a opposite the vertex x. Wayne gave a verbal rendition of this formula:
| (1) Wayne: | You pick any vertex and it’s going to be the two sides that make the angle, subtract the side opposite the angle, and divide by two. I understand everything except why you divide by 2. |
***
(2) Ben: You know why you divided by 2, is because-
(3) Rachel: Because there’s two sides.
(4) Ben: No. No, it’s because-
(5) Wayne: There’s two other points, to be solved for, no?
(6) Ben: No. No. No. We found out that Y, X + Y + Z is half of the outside points.
(7) Wayne: That’s right!
***
(8) Ben: So if you’re trying to find one point you add the two-
(9) Wayne: The two sides-
(10) Ben: -adjacent sides and then-
(11) Wayne: -that angle. The two sides that come in-
(12) Ben: -Yeah, the angle.-
(13) Wayne: -to that point to make that angle, OK Adjacent.
(14) Ben: -minus the opposite.
| (15) Wayne: | And divide by 2 because we found out that the ratio for sides added together, plus points added together was 2. |
(16) Rachel: Was 2.
(17) Ben: The ratio is one half.
(18) Wayne: And since we’re trying to find a point,
(19) Eleanor: This is half of this.
(20) Wayne: -that’s why it’s a half, over a half.
In line 1 Wayne wants an explanation: “Why you divide by 2?” After a short discussion of the differences between the way Wayne describes the process and Rachel’s equation (omitted from the transcript), Ben attempts an explanation (see lines 2-7). He is interrupted by explanation from both Rachel and Wayne.
Rachel’s explanation (line 3) might be analogical or deductive. She may be referring to an analogy between the two sides adjacent to the vertex to be solved and the divisor 2. But it is more likely that her explanation is deductive, given that she derived the original equation algebraically. She began her derivation by adding the two equations referring to the vertex x:
When the 2 appears in the third line, it is because x is involved in the totals of two sides, b and c. When the derivation is completed the 2, which came from the combination of two sides at the beginning, becomes the 2 that is divided by at the end. Rachel’s explanation is deductive for no one but her since her short comment is not sufficient to really communicate it to them or to Eleanor. In fact, it is likely that if they considered her explanation at all, they took it to be a weak analogy.
Wayne’s explanation (line 5) works only by analogy. There are two more vertices to be solved, once the first is known, but there is no connection between the division by 2 and the number of vertices remaining to be solved, other than the number 2. This makes this a weak analogy. It is interesting that even though Wayne had been the first to voice a need to understand the division by 2, a minute and a half later he seems more anxious to suggest his own explanation than to hear Ben’s.
Ben’s explanation (line 6) might be analogical or deductive, but it seems more likely that it is analogical. There is no evidence that Ben spent time making a deductive connection between Rachel’s equation and the relation which he had discovered empirically with Eleanor and Wayne: a + b + c = 2(x + y + z). Here the analogy is stronger than in Wayne’s explanation since the analogy is between two
equations with variables instead of between an equation and a state of affairs. This strength is likely to have led to Wayne’s acceptance of Ben’s explanation over his own.
The explanations that were rejected were a weak analogy (Wayne’s) and a deductive explanation that was taken by the rest of the students to be a weak analogy (Rachel’s). The students preferred the strong analogy, which was based on several points of connection. This is sensible since a strong analogy could have (and in this case does have) the potential to be developed into a deductive proof. In the end (at line 15) it is this strong analogy that is accepted as explaining why the division by 2 occurs.
It is worth noting that even though Rachel’s explanation was the most thought out and based on deduction rather than analogy, which might suggest it was a more certain explanation, it was apparently not even considered by the others. This illustrates a weakness of proving versus analogy for explaining. Proving is a process that must be formulated to be communicated and must be followed with some care to be understood. In this situation the social dynamic did not afford Rachel the opportunity to make her case clearly. Ben’s analogy, on the other hand, could be understood immediately by Wayne and Eleanor, who were familiar with the context to which he was making links. Rachel could also see these links after Eleanor showed her what formula was being referred to (line 19).
Summary
Explaining can be done by proving and by analogy. Explaining by proving can be more or less formulated. Whether explaining is successful depends not only of the method of explaining but also on the social context.
Unformulated explanations are limited precisely because they are unformulated. As explanations for other people they are useless, as Ben’s attempt reveals. As explanations for an individual, they may work, but only if the argument required is very short. These same weakness show up in unformulated proving used to explore (see section 2).
Formulated proving allows extended explanations beyond what analogy can provide. At the same time, formulated proving is not necessarily preferred over explaining by analogy (as in the case of Bill). In some contexts, where no strong analogies occur, formulated proving may be the only method of explaining possible. At the same time, formulated proving to explain seems to require an appropriate social context, either one in which it is already occurring to address another need, or one in which there is a strong need to explain to others, or one in which a teacher (present or in the past) indicates that formulated proving should be used.
Analogies can be described as strong or weak. A strong analogy can satisfy a need for explanation. In fact, a strong analogy can be preferable to a deductive explanation, either because it is more easily communicated, or because it occurs first and removes the need to prove to explain.