previous        table of contents        next

---

CHAPTER I

PROOF AND PROVING

Prove all things; hold fast that which is good.

— I Thessalonians 5, 21

This chapter explores two questions, by way of introducing the ideas I will be considering as part of my larger exploration of the need to prove.  The first of the questions is, “What is proving?”  The second is, “Why do people prove?”  In the two sections of this chapter I will only be able to begin trying to answer these questions, but I do hope to clarify exactly what is being asked.

1. What is proving?

The simplest answer to this question might be “Proving is making a proof.”  This answer leaves us free to talk about proofs.  Talking about proofs is easier than talking about proving, just as talking about books is easier than talking about writing.  If my original question had been “What is a proof?” we could have begun with a few examples.  This is precisely the approach taken by the professor in a vignette by Davis and Hersh (1981. p. 39), when asked “What is a mathematical proof?”.  There has been a great deal of research done in mathematics education on proof, especially on teaching students to read and write proofs, and on their difficulties in doing so.  There has been very little research on proving, the reasoning processes that the proof embodies.  It is not that proving is uninteresting.  It is just that proofs are a lot easier to observe, to talk about, and to write about.   If I were researching proofs I could show you the proofs that were produced in my studies.  Strictly speaking, I cannot show you proving (although I will be trying to do so with transcripts of students’ proving).

Nevertheless, it is important that I am researching proving.  Rather than saying “Proving is making a proof,” I would rather say “A proof is what results from proving.”  This emphasis on proving is a consequence of my belief that the teaching of proving must begin with students’ existing reasoning processes, and with an awareness of the circumstances in which they reason deductively.  In the next chapter it will become apparent how this emphasis affects my research. 

So, what is proving?  In Thessalonians, Paul the Apostle advised “Prove all things.”  Paul was not, so far as I know, an obsessed mathematician.  His suggestion simply means that we should investigate.  “Prove” is derived from probare, which means to test, to try.  The verb “probe” still carries this meaning, although it also conjures images of poking with sticks.  The sense of probare is part of what proving is: investigating.  But proving is investigating in a certain way, and to get at that aspect of what proving is, I will, after all, have to talk about proof.

In some common phrases, “proofread,” “proof of the pudding,” “100 proof,” the word “proof” still holds onto the meaning of investigation, but there is another common usage of proof.  When we doubt a statement, we may ask, “Do you have any proof of that?”  In this question “proof” means evidence.  Often the evidence is expected to take the form of a deductive argument from some agreed upon premises to the desired conclusion.  This especially true in the sciences and in

 

mathematics.  This deductive aspect of proof indicates the way of investigating that I call proving.

The contrast between everyday uses of the word “prove” and the more precise meaning I give it is illustrated by the expression “the exception which proves the rule.”  This expression is usually taken in the paradoxical sense of asserting that the presence of a single counterexample to a generalization establishes the universal truth of that generalization.  “Prove” is taken to mean providing evidence, without any reference to reasoning about the situation.  This expression was not always so paradoxical.  In fact, if we remember that proving originally referred to investigating a situation, saying “the exception proves the rules” amounts to suggesting that examining exceptions closely, reasoning out the way they occur, can lead to a clarification and improvement of the rule.  Lakatos (1976) elaborates this process in some detail, in his analysis of the ways in which counterexamples and proving interact to improve theorems in mathematics.

In summary, proving, for me, is investigating using deductive reasoning.  Deductive reasoning refers to reasoning that proceeds from agreed upon premises to conclusions, using logical arguments.  I will not be using proving to mean investigating in non-deductive ways, nor will I be restricting proving to reasoning deductively to provide evidence.  I hope the reader will agree that this interpretation of proving is useful, in light of the ideas it permits me to present in the following chapters.

Although proving is a part of reasoning in many fields, I am particularly concerned with proving in mathematics, and so it seems advisable to look at what proving is in mathematics.  As mathematics in schools is necessarily different from what professional mathematicians do, I will briefly mention what proving is in  schools, both in the curriculum and in students’ own understandings, before describing what proving is to mathematicians.  

What is proving in school mathematics?

In schools “prove” is often used loosely, as it is in everyday life.  It can also have a much more restricted meaning.  The authors of Alberta’s curriculum documents define “prove” in this way: “Prove: to substantiate the validity of an operation, solution, formula or theorem in general and to provide logical arguments for each step in the process” (Alberta Education, 1991, p. 5).  This meaning of proving is concerned with providing evidence, with substantiating validity.  No longer are the experimental techniques once used to “proof” rum appropriate.  Proving here is logical, deductive, certain, and general.  In addition the stress has shifted from the action of proving to the result, certain knowledge of the validity of a statement. 

Students often use “proving” to mean providing evidence, without distinguishing how that evidence is obtained.  This is startlingly illustrated by the comments of students interviewed by Finlow-Bates (1994).  Consider the following exchange (K is Finlow-Bates, T is a university student):

            K:        And the examples, what are they there for?

            T:         Just to prove, prove the statement.

            K:        What does that mean, “they prove the statement”?

            T:         They prove, that means they make it true.

 

            K:        So the ...

            T:         (interrupting) under all conditions.  (p. 348, emphasis in original)

For this student “prove” means to make a statement true, and the inductive evidence provided by examples is sufficient to do so.  We will see other examples of this association of “proof” with verifying in the next chapter.

What is proving for professional mathematicians?

Proving is a means of coming to understand, and of coming to know what understanding is.  In trying to prove something new, one is asking what makes it tick; in trying alternative proofs, rejecting them, modifying them, one is discovering things about its structure—and solidifying one’s knowledge in the process.  This is the deep reason for much of the emphasis on proof in mathematics.  The mathematician comes to accept proving as a way (if not the way) of thinking, a way of demanding and insuring that he does indeed understand.  (Schoenfeld, 1982, p. 168, emphasis in original) 

Professional mathematicians prove as an integral part of their occupation.  Lakatos (1976) describes the process of mathematical discovery as a cycle of conjecturing, making a proof, and testing with counterexamples.  This process can begin at any stage in the cycle.  For example, a conjecture can be made for which a proof is offered, and then a counterexample is found that forces a revision of the conjecture or the proof, so a new conjecture or proof is made, and the cycle continues.  Alternately, proving could lead to a new result, so that the proof and the conjecture arise together.  The discovery of a counterexample then returns the cycle to proving anew.  While Lakatos does not consider beginning the cycle with a counterexample, a cycle could begin there, as in the case of a counterexample to an implicit generalization.  An example is De Morgan’s discovery that the digit 7 occurs less often than one would expect in the decimal expansion of p, which marks the origin of a cycle of proofs and refutations involving the degree of randomness to be expected in p.

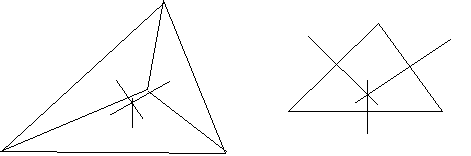
Figure 1: Intersecting perpendiculars.

While conjecture, proofs, and counterexamples can all arise from proving, proving is not the only way of investigating used by mathematicians.  The importance of analogical and inductive reasoning in mathematics has been described at length by Polya (1968).  Reasoning by analogy involves making a conjecture based on similarities between two situations.  For example, one might conjecture that the perpendiculars through the centroids of the faces of an irregular tetrahedron 

 

meet in a point, by analogy to the perpendicular bisectors of a triangle (see Figure 1).

Inductive reasoning is characterized by the making of a generalization from a pattern noticed in several specific cases.  The classic example is making the generalization “The sun will rise every day” from several million specific cases.  A more mathematical example would be generalizing “The product of two consecutive numbers is always even” from the cases 3x4=12, 4x5=20, 12x13=156, and 37x38=1406. 

Lakatos developed his cycle of proofs and refutation to accurately represent what proving is to mathematicians.  He did so in opposition to what he called the Euclidean model, which portrays mathematical research as a process of beginning with a set of assumptions, and then proving theorems from them with absolute certainty.  This image might be derived from the assertions of Formalist philosophers of mathematics (see Chapter VI, section 2).  The Euclidean model bears a superficial resemblance to a cycle that begins with making a proof.  It lacks, however, any role for counterexamples.  In the Euclidean model mathematical discovery is seen as a steady forward progress from truth to truth, not a recurring cycle of proof and refutation.

Another mistaken image of what proving is to mathematicians portrays proving as the verification of mathematical discoveries that are made through other ways of reasoning.  This image is often associated with the teaching of mathematics.  For example the NCTM Standards (NCTM, 1989) state:

A mathematician or a student who is doing mathematics often makes a conjecture by generalizing from a pattern of observations made in particular cases (inductive reasoning) and then tests the conjecture by constructing either a logical verification or a counterexample (deductive reasoning).  (p. 143)

If a cycle of proofs and refutations begins with the making of a conjecture then that cycle looks something like this “discover, then prove” image.  It differs from this image both in its cyclical character, and in that conjectures can arise through proving, as well as through inductive or analogical investigations.

This may be an appropriate place to mention that the question “What is a proof?” is an important one in mathematics.  This question is related to two issues, the degree of formality of a proof, and the sort of proving that produced the proof (see Chapter VI, section 2).  Formality became important in the early twentieth century, when formal proofs were seen as more reliable than informal proofs.  The sort of proving involved in producing a proof has become important with the increase in the use of computers in mathematics.  The character of proving by working through an argument oneself differs from proving done by setting up a computer to check all possible cases.  Concern over the nature of proof also arises when a proof is the product of many individuals working on related topics, so that a conclusion might be reached without any one person ever having proved it entirely.

Lakatos (1978, p. 61) introduced the terms pre-formal, formal, and post-formal to describe proofs of different degrees of formality.  I would further divide formal proofs into semi-formal and completely formal proofs, a distinction pointed out to me by Uri Leron.  A pre-formal proof might appear in the working notes of a mathematician.  It may involve hidden assumptions, and use informal language 

 

and notation.  It might also include references to analogical or inductive evidence for the conjecture.  A semi-formal proof is presented in a form suitable for publication in a professional journal or a textbook.  The arguments are purely deductive, and unusual assumptions are made explicit.  Some steps might be omitted however, with a note to the reader suggesting how they may be worked out.  The proof is written in a mixture of formal symbols and natural language.  A completely formal proof might also appear in a journal, or as a computer program.  In a completely formal proof all steps are included, and all assumptions are made explicit.  The language of the proof is entirely symbolic.  A post-formal proof talks about the nature of formal proofs, from a meta-mathematical perspective.  They may resemble pre-formal or semi-formal proofs, but they will also include elements from the formal system that is the object of the proof.  The proof of Gödel’s Theorem is a well known example (see Chapter VI, section 2).

2. Why do people prove?

It is impossible to give a single reason why people prove.  Proving occurs in widely different circumstances, with different goals.  Within groups, however, one can begin to see some common purposes for proving.  Because proving is so important in mathematics, I would like to begin by focusing on the question “Why do mathematicians prove?”  The more complicated question, “Why do students prove?” is central to my research.  I will consider it at the end of this section and in the next three chapters.  In Chapter VI I will return again to the general question of why people prove, and by that point it may be possible to hint at some answers.

Why do mathematicians prove?

Ulam (1976) hints at the answer to this question when he states that “Georg Cantor proved (i.e., discovered) that the continuum is not countable” (p. 282).  Cantor’s discovery came through proving.  Lakatos’ (1976) historical analysis of the use of proving in mathematics reveals that mathematicians in general employ proving to both discover and improve propositions.  The use of proving to discover, which Lakatos calls “deductive guessing,” involves a cycle of proofs and refutations in which the proving is both the source of the conjecture and part of the process of testing it.  As Lakatos wrote:

There is a simple pattern of mathematical discovery — or of the growth of informal mathematical theories.  It consists of the following stages:

(1) Primitive conjecture.

(2) Proof (a rough thought-experiment or argument, decomposing the primitive conjecture into subconjectures or lemmas).

(3) ‘Global” counterexamples (counterexamples to the primitive conjecture) emerge.

(4) Proof re-examined: the ‘guilty lemma’ to which the global counterexample is a ‘local’ counterexample is spotted.  This guilty lemma may have previously remained ‘hidden’ or may have been misidentified.  Now it is made explicit, and built into the primitive conjecture as a condition.  The theorem — the improved conjecture — supersedes the primitive conjecture with the new proof-generated concepts as its paramount new feature.

 

These four stages constitute the essential kernel of proof analysis.  But there are some further standard stages which frequently occur:

(5) Proofs of some other theorems are examined to see if the newly found lemma or new proof-generated concept occurs in them: this concept may be found lying at cross-roads of different proofs, and thus emerge as of basic importance.

(6) The hitherto accepted consequences of the original and now refuted conjecture are checked.

(7) Counterexamples are turned into new examples — new fields of inquiry open up.  (1976, p. 127)

This use of proving to discover is doubtless the central reason why mathematicians prove.  Thurston (1995), in relating something he learned as a graduate student about mathematicians, mentions other reasons.  “I thought what they sought was a collection of powerful proven theorems that might be applied to answer further mathematical questions.  But that’s only one part of the story.  More than knowledge, people want personal understanding.  And in our credit driven system, they also want and need theorem credits (pp. 35-36, emphasis in original). 

The importance of proving as a mark of mathematical activity should not be underestimated.  The criticism of Mandelbrot by Krantz (1989), in which Krantz charged that Mandelbrot’s investigations of fractal geometry were not a part of mathematics because Mandelbrot proves no theorems, illustrates this use of proving as a marker.  The exclusion of non-Europeans from the history of mathematics, on the same basis that they did not prove their work (Gheverghese Joseph, 1991), is another example.  Proving in this context can be seen as conferring status on a mathematician, as a stethoscope does on a doctor.  Mathematicians form a society with customs and rituals, just as other groups of people do, and the rite of initiation is the creation of an original proof.

I have not mentioned a reason to prove that many people would see a central to mathematics: verifying that theorems are true.  The influence of this idea can be measured by reference to Crowe’s (1988) list of “ten misconceptions about mathematics.”  It is included in Crowe’s list twice, once as “mathematics provides certain knowledge,” and the second time as “mathematical statements are invariably correct.”  It is a misconception for two reasons: 1) Proving does not always verify, and 2) Methods other than proving are often used to verify theorems.

Proving does not always verify

The status of proving as the path to absolute certainty has suffered some serious setbacks in the last two centuries, and this process continues.  The discovery of non-Euclidean geometries, which contradicted the claim that Euclidean geometry describes with certainty, was the first setback.  The paradoxes of set theory offered the second setback, and Gödel’s Theorem set bounds on the certainty proving could provide (Kline, 1980; see also Chapter VI, section 2).  More recently, the proliferation of proofs in mathematics journals, the increasing length of proofs, the specialization of the field, and the increased use of computers, have highlighted the human and social elements of the uncertainty of proving.

Ulam (1976, p. 288) estimated that in the early 1970s, almost 200 000 theorems were published each year.  Davis (1972/1986) pointed out the stress this puts on the process of refereeing proofs, leading to the suggestion that half of the proofs published might be flawed.  Although this suggestion was originally made 

 

to Davis in jest by an editor of Mathematical Review, it has been widely quoted as correct, presumably because it seems quite plausible to members of the mathematical community.  Recently, the case of Wiles’ proof of Fermat’s Last Theorem (see below) has added further evidence as to the unreliability of published proofs.  The careful checking of Wiles’ proof resulted in the discovery of errors in several of the proofs to which he made reference.  Given this, it is hard to justify a claim that we are certain of the 200 000 theorems published in 1970, even though they have been proved.  At best we can ascribe a probability of certainty to them.

Part of the difficulty in deriving certainty from contemporary proofs in mathematics is their length.  The elusive property of elegance in proofs includes an inclination towards short proofs.  A joke claims that a Ph.D. thesis in mathematics should be rejected if it runs over ten pages.  This preference for brevity is not merely aesthetic, however.  There are sound practical reasons for mathematical proofs to be short.  Chief among these is the requirement of surveyability.  For a proof to be surveyable it ought to be possible for a suitably trained mathematician to consider the whole proof at one time.  Many contemporary proofs stretch this requirement.  The most extreme example thus far is the cataloguing of the simple finite groups.  The proofs cover over 5000 journal pages, and none of the mathematicians involved can be said to have surveyed the complete proof (Davis & Hersh, 1981, p. 388).

A further difficulty in achieving certainty through proving is the increased specialization of mathematics.  Many proofs concern topics or employ techniques so abstruse as to be incomprehensible to the vast majority of mathematicians.  This problem is a steadily worsening one.  It is said that Poincaré, who died in 1912, was the last mathematician to have a sound grasp of the entire field (Boyer, 1968/1985, p. 650).

The problems of length and specialization can be illustrated by a consideration of the recent proof of Fermat’s Last Theorem by Wiles (originally described by him at Cambridge in 1993, and outlined by Ribet & Hayes in American Scientist in 1994.  The original, flawed, proof has been repaired, but is as yet unpublished).  The proof is very long, running to about 200 pages (Ribet & Hayes, 1994, p. 156), and makes use of several mathematical specializations: elliptic curves, Galois groups, deformation theory, modular forms, etc.  There are few mathematicians with the background to referee Wiles’ proof, and its complexity and length make their task difficult.  If the proposition were a less celebrated one, it is doubtful the resources being devoted to checking the proof would have been available, and the errors detected so far might have gone uncorrected.

The proof of Fermat’s Last Theorem also demonstrates another aspect of the role of proving in providing certainty.  Prior to the announcement of Wiles’ proof few mathematicians would have doubted that Fermat’s Last Theorem is true, based on the considerable empirical evidence amassed in the three centuries since Fermat proposed it.  It is known, for example, that Fermat’s Last Theorem is true for all numbers less than 4 million.  Fermat’s Last Theorem also has a quality, which could be described as plausibility.  In mathematics, exceptions to simple generalizations  usually are discovered quickly, if they exist. The truth of Fermat’s Last Theorem for n = 3 or 4 made it plausible that no other exceptions would be found.  Given that everyone expected Fermat’s Last Theorem to be true, in what sense can Wiles’ proof be said to have increased the certainty of its truth?

The use of computers in math has radically changed the way we see proof in mathematics.  This has occurred in two ways.  Computers have introduced a powerful new tool for proving mechanically, analogous to algebra and calculus, but not as yet enjoying the same degree of acceptance.  In addition, computers have allowed mathematicians to visualize mathematical situations before proving in those situations.

I have been fortunate to been working in mathematics in the years when  two fascinating theorems first were proved: Fermat’s Last Theorem, and the Four Colour Theorem.  Both of these propositions are easily stated, but difficult to prove.  The proof of Fermat’s Last Theorem is long and complicated, but traditional in form.  The proof of the Four Colour Theorem, on the other hand, provoked controversy because of the extensive use of computer algorithms in it.  Because of the use of this novel technique of mechanical deduction many mathematicians rejected the proof as invalid.  This added another element of uncertainty to use of proving to verify.

The proof of the Four Colour Theorem could be criticized on the basis of its unsurveyability, due to its length, or the specialist backgrounds required to understand it; however, the chief critique focused on the possibility of programming or computer error.  This is a general weakness in any form of mechanical deduction.  A misprint in an algebraic derivation or a computer program can be made easily, have radical effects, and be almost undetectable.  As a result, in practice the validity of a proof must often be determined in other ways.

Other ways mathematicians verify

Hanna (1983) describes five ways in which she believes mathematicians verify propositions:

Most mathematicians accept a new theorem when some combination of the following factors is present:

1. They understand the theorem, the concepts embodied in it, its logical antecedents, and its implications.  There is nothing to suggest it is not true;

2. The theorem is significant enough to have implications in one or more branches of mathematics (and thus important and useful enough to warrant detailed study and analysis);

3. The theorem is consistent with the body of accepted mathematical results;

4. The author has an unimpeachable reputation as an expert in the subject matter of the theorem;

5. There is a convincing argument for it (rigorous or otherwise), of a type they have encountered before.

If there is a rank order of criteria for admissibility, then these five criteria all rank higher than rigorous proof.  (p. 70)

Note that most of these are based in the human and social nature of mathematics, not on the use of proving to produce certainty.

Why do students prove?

Some readers may question the wisdom of asking “Why do students’ prove?” when it seems quite possible that students do not prove.  To begin, then, I will give some examples of students’ proving from my own work and from the mathematics education literature.  I will then review the answers given in that literature to the question “Why do students prove?” with some comments on the plausibility of those answers.  The next chapter explores my own attempts to investigate students’ need to prove in detail.

Do students prove?

When “proving” is taken in the restricted sense of “producing semi-formal proofs” very little proving is witnessed.  But if “proving” is taken to refer to deductive reasoning, evidence abounds that students can and do prove in and out of mathematical contexts.  In this section I will be mainly concerned with what I call “unformulated proving,” proving that is informal and only partially articulated.  A more detailed description of unformulated proving occurs in the next chapter.

In the mathematics education literature the main focus is on proofs rather than proving.  This has limited the amount of published discussion of unformulated proving.  There are, however, several indications that unformulated proving is a known phenomenon.  Balacheff (1991, p. 179) mentions that students show “some awareness of the necessity to prove and some logic” in their behavior outside of school.  Edwards (1992) comments:

Some students at the beginning of high school, even without instruction in formal proof, will go beyond empirical reasoning and offer informal proofs, or explanations, of their findings.  (p. 215)

Blum and Kirsch (1991) describe “preformal” proofs, which they claim students are generally able to construct, based on “intuitions” that are common to all students.  Moore (1990, 1994) also observed students who could prove informally, and examined some of the elements of their difficulties in making their proving more formal.  “Examples, concept images, and informal approaches were helpful, and often necessary, for discovering a proof, they did not guarantee that a student could write a correct proof” (1994, p. 257, emphasis in original).

In my own research (Reid 1992, 1993) I have seen unformulated proving by students from a wide range of school levels and mathematical abilities.  A particularly clear example appears in Reid (1992).  Beth, a university humanities undergraduate, who last took mathematics in grade 11, gave this argument that every third Fibonacci number^* is even:

 

(1) Beth:          This one, at least I think I know why, the multiples of three work out to be even because the, the other two,    when you add the Fibonacci numbers the other two are odd and then so it would come out to be even.

(2) DR:            How do you know the other two are going to be odd?

---

(3) Beth:           I don’t — that again is looking at the little charts and they seem to work out that way —

(4) DR:             So you’ve made a conjecture that, the two Fibonacci numbers before one that is a multiple of three will both  be odd.

(5) Beth:           Because, no, because you-  If each Fibonacci number is the first one plus the second one equals the third one, — the first, it starts out, well, then you would be adding two odd numbers together and get an even number, and then you add, oh, that’s the same thing, I see, you’d say, then the next one then is odd, so you’d add that to the even and then you’d come out to another odd, but then I don’t necessarily know that the, that the next number after an even number would be odd so —

(6) DR:             Can you think of any reason why the next one after an even number should be odd?

(7) Beth:           — because the one before the even number was odd  (p. 319)

In my current research (described in the next chapter) unformulated proving was used by all the participants, including Sandy, a mathematically talented student in grade six, and Bill and John, two mathematically weak students in grade 10.

Uses of proving

Many uses of proving have been mentioned in the mathematics education literature.  They include:

Verification — Fischbein and Kedem (1982), Bell (1976), and many others

Explanation — Hanna (1989), de Villiers (1991), Bell (1976), Moore (1990)

Exploration — de Villiers (1990)

Systematization — Bell (1976)

Communication — de Villiers (1990), Arsac, Balacheff and Mante (1992)

Aesthetics — de Villiers (1990)

Personal self-realization — de Villiers (1990)

Developing logical thinking — de Villiers (1991)

A “teacher-game” — Alibert (1988), Schoenfeld (1987)

In a survey of prospective teachers de Villiers (1991, p. 23) found that most (61%) felt  that the main function of proof is verification. Other popular categories were explanation (7%), systematization (11%), and developing logical thinking (4%). Moore (1990) found that college students only listed verification and explanation as functions of proof.  In contrast to de Villiers’ teachers, Moore’s students proposed explanation and verification in approximately equal numbers (5 explanation, 6 verification, p. 113).  Each of the uses listed above will be described in more detail in the following paragraphs.

Teachers often tell students that proving verifies that a mathematical proposition is true.  In doing so we echo a traditional definition of proof as something that establishes truth.  The need to verify as a motivation for proving appears in almost all research about proof and proving (see Appendix A).  This motivation for proving has also provided mathematics education researchers with a 

methodology to determine understanding of proving.  For example, Fischbein and Kedem (1982) tested understanding by asking students who had seen a proof whether they would care to examine other confirming examples of the proposition.  Students who requested additional empirical data were deemed not to understand proof, as they had not understood that proving establishes certainty.  According to this criteria, mathematicians such as Crowe (1988), who does not believe that proving establishes certainty, would also be deemed not to understand proof.

Finlow-Bates (1994) has done some research that suggests that the students Fischbein and Kedem studied might have learned to request additional examples in school.  In his study five students were asked to select the “best” proof from a set of four.  The four proofs included a set of examples, a proof, a proof preceded by examples, and a proof followed by examples.  Although three students chose the proof alone when first asked, the suggestion that they provide a reason for their choice caused them to switch to the proof followed by examples. In the final rankings all five students rated best the proof followed by examples, with the examples followed by the proof ranked second best.  Although the reason for the students’ choice is not obvious, it seems plausible that they were reflecting the normal presentation they had seen in school where teachers often state a general principle, explain it, and then give examples.

Research has suggested that only a few students see verifying as a use of proving; most students do not (Bell, 1976; Braconne & Dionne, 1987; Fischbein, 1982; de Villiers, 1992; Senk, 1985).  Using verification to motivate proving in schools may play a significant role in students’ difficulties in learning to prove.  The fiction of proving as the path to complete certainty is a fiction, and students may be quicker than their teachers to recognize this. 

Hanna (1989) and de Villiers (1991) both stress the importance of proving as a way of explaining in educational contexts.  Hanna asserts that proofs used by teachers in lessons should be picked on the basis of both their explanatory and verificatory qualities.  De Villiers claimed that students have a need for explanations and will accept proofs as explanations.  Unfortunately, de Villiers’ research is not sufficient to indicate that students would feel a need for explanation in all mathematical contexts, nor did he consider whether students themselves would employ proving to explain.  In my research I have attempted to investigate these questions further (see Chapter II).

De Villiers (1990) asserts that proving is an important means of exploring in mathematics.

Even within the context of such formal deductive processes as a priori axiomatization and defining, proof can frequently lead to new results.  To the working mathematician proof is therefore not merely a means of a posteriori verification, but often also a means of exploration, analysis, discovery and invention. (p. 21)

De Villiers goes on to give examples of theorems in geometry that students could discover through deductive exploration.  The use of proving to explore is also implicit in the teaching methods proposed by Fawcett (1938) and Lampert (1990).

Systematization consists of “the organisation of results into a deductive system of axioms, major concepts and theorems, and minor results derived from these” (Bell, 1976, p. 24).  De Villiers (1990) mentions the importance of 

systematization for mathematicians, but he presents no evidence that students would prove to satisfy a need to systematize.

Communication is also suggested by de Villiers (1990) as a possible reason to prove.  Arsac, Balacheff & Mante (1992) provide examples of students proving as communication, in the context of an activity which asked them to focus specifically on communicating mathematical ideas.

De Villiers (1990) briefly mentions aesthetics and personal self-realization as reasons to prove, but he does not elaborate. Presumably he meant these to correspond to needs felt by professional mathematicians.

Developing logical thinking was once an often stated goal of teaching proof (see Fawcett, 1938, for a summary of such assertions).  Although research (e.g., Sekiguchi, 1991, p. 26) indicates that there is little transference of proof skills learned in mathematics to other contexts, some teachers (4% according to de Villiers, 1991,  p. 23) still believe that this is the primary function of proof. 

A teacher-game is an activity that earns marks and acceptance, but is seen as being otherwise useless.  Alibert (1988) and Schoenfeld (1987) describe proof having this function for  students.  Teacher-games are described in more detail in Chapter II, section 4.

Researching the need to prove

The needs listed above are all possible answers to the question “Why do students prove?” but a more precise answer is needed.  If teaching is to be based on an understanding of students’ needs, then that understanding must include an idea of which needs are most important, and what circumstances occasion those needs.  Developing this understanding is the goal of the studies I report in the next three chapters.  Before considering those studies, however, let me recall two basic assumptions on which my research is based.

First, I assume that what people learn is based on what they already know.  In fact, to make this statement a bit stronger, I assume that what we can learn is based on what we already know.  This assumption is at the base of constructivist learning theory, and Enactivism, a theory of learning I will be describing at length in Chapter VII.  A consequence of this assumption for education is that teaching ought to be based on what students know.  In the context of teaching mathematical proof, this means that the proving we would like students to do should be based on the proving they already do, not developed as a disconnected skill unrelated to any other way of thinking.  This assumption also has a consequence for my research, in that I concentrate on the proving in which students engage without any instruction from me.  The studies I conducted occasionally touched on the possible effects of teacher interventions on students’ proving, but the main focus was the reasoning students were inclined to do based on whatever previous experiences they had.

Second, I assume that people reason in different ways in different contexts and that seemingly similar contexts can, and often do, turn out to be different enough to give rise to different reasoning.  For this reason I am not interested in searching for the context in which students’ prove.  I am interested in exploring possibilities, not generalities.  This interest had consequences for the way I conducted my studies.  It occasioned the use of open problem situations, in which 

deductive reasoning could be used, but was not required.  It also occasioned the involvement of a wide range of students, both in age and ability. 

Before describing the studies, and my results, a brief note on the contents of the next few chapters is in order.  It is usual in dissertations to describe in detail the design of the studies undertaken before presenting the results of the studies.  This is sound practice if an important feature of the research being conducted is reproducibility.  For a legitimate attempt at reproducing a study to be made, it is necessary that the design of the study be clearly understood. 

In the case of my studies the situation is a bit different.  My conclusions are of two kinds: observations and speculations.  My observations consist of claims that one or more of the participants in my studies reasoned in a particular way.  Such observations are clearly not reproducible, as the context can never be replicated. To do so would require a replica of the participant involved, and not even the original participants continue to encompass all the aspects of who they were at the time.  My observations show what is possible, but do not allow predictions of what will happen.  All the same, suggesting ways to improve teaching must be based on some sort of reasons, and in many cases these reasons take the form of predictions of the wonderful things that will result if such-and-such a reform is introduced. 

This is where my speculations come in.  Based on both the observations I have made, and philosophical considerations, I indulge in some speculations as to ways the teaching of proving could be reformed.  I do not, however, claim that these speculations are based on reproducible evidence.  In fact, I would suggest that the best way to test my conclusions as they apply to teaching is not to attempt to replicate my results (I would be far more interested in studies that expanded the bounds of the possible by observing proving in situations I failed to investigate),  but rather to attempt to implement my speculations in practice.  It could be suggested that experimenting with new methods of teaching, without having “scientific” evidence of their effectiveness beforehand, is irresponsibility on the part on an educator.  In response I would note that the results of research on students’ understanding of proving in mathematics (e.g., Bell, 1976; Braconne & Dionne, 1987; Fischbein, 1982; de Villiers, 1992; Senk, 1985) indicates that current methods are so unsuccessful that it is difficult to imagine students suffering much under a change.  I would also note that it may be impossible to acquire “scientific” evidence in some contexts (I expand on this idea in Chapter VI) and so limiting educational reform to those based on such evidence might permanently cripple our educational systems.  

With the above comments in mind, I have left the details of the design of my studies to an appendix (Appendix B).  Below I will give an introduction to the studies, and in the following chapters I will describe aspects of the studies as they become needed.  In doing so I will concentrate on the particular, in keeping with overall focus of my research.  Those who would prefer an overview should consult Appendix B now, and Appendix D when a summary of results is desired.

In Chapter VII I make some important connections between how I did my research and the theoretical basis for my thinking.  It could be suggested that an understanding of my methodology and the theoretical basis of it is important to the reading of the results I have included in the next three chapters.  This may be, but it is also the case that the contents of the next three chapters are important to the reading of my final chapter.  Enactivism, the topic of Chapter VII, is not a theory or 

a methodology in the abstract.  It must be about something.  In Chapter VII it is about my research into proving.  The reading of the next three chapters may raise important questions about theory and methodology, the existence of which will give the answers given to them in Chapter VII a context and motivation.

Although there is a great deal of research in mathematics education on the types of proofs students make and accept, on the teaching of proving, and on students’ acceptance of proofs as absolute verification, the only studies that have concentrated on students’ need to prove have been those of Bell (1976), Hanna (1989), and de Villiers (1990, 1991).  None of these observed students’ proving in contexts in which proving was possible but not required.  As it seems to me that it is only in such situations that students’ needs to prove will become apparent, I have attempted in a series of research studies to observe students in such contexts. 

The students involved in my studies were volunteers from high school and university classes.  They represent a wide range of mathematical backgrounds, from students with undergraduate degrees in mathematics, studying to become teachers, to students in the non-academic stream of grade 10.  In addition to taking part in problem solving sessions, high school students were also observed in their regular classrooms, to get a sense of what their typical experience of proving in mathematics is like.

The studies included observations of three high school classes, observations of students in problem solving situations, and interviews with those students.  Three problem situations were investigated: the Arithmagon, the Fibonacci sequence, and GEOworld.  Prompts used for the Arithmagon problem and the Fibonacci situation are given in Figures 2 and 3.  GEOworld is a computer microworld, that will be described when students’ activities in that situation are discussed.  These problems were selected based on their having occasioned proving in previous studies (e.g., Reid, 1992) and pilot studies.  It might be helpful for the reader to investigate these problems before continuing, in order to have a better feel for the students’ reasoning^*.

Figure 2: The Arithmagon prompt.

---

Figure 3: The Fibonacci prompt.

After investigating the problems, in separate sessions, the students were interviewed. 

As I mentioned above, the next three chapters elaborate on the studies I conducted into students’ proving and need to prove, and the results of these studies.  Most of the examples in these chapters are transcribed from video tapes of the problem sessions and interviews.  A few examples are taken from the observations of high school mathematics classes.  Introducing all the students I observed at once could be confusing, and is unnecessary, as my analysis concentrated on the particular rather than the general.  I have taken most of my examples from the observations of three pairs of university students, two pairs of high school students at North School, and Sandy, a male grade six student.  The university students included one male-male pair (Ben and Wayne), one female-female pair (Eleanor and Rachel), and one female-male pair (Stacey and Kerry).  Both pairs of high school students are male.  Bill and John were in grade 10.  Colin and Anton were in grade 12.  Descriptions of the students and their mathematical backgrounds is given in Appendix B.