previous        table of contents        next

---

CHAPTER V

TEACHING PROVING

Histories make men wise; poets, witty; the mathematics, subtle; natural philosophy, deep; moral, grave; logic and rhetoric, able to contend.

— Francis Bacon, Essays,

50. Of Studies

The importance of teaching proving has long been recognized by mathematics educators and curriculum designers.  The difficulty of teaching proving also has been recognized, and research focused on improving the teaching of proving dates back at least sixty years (e.g., Fawcett, 1938).  The insights into students’ need to prove provided by my research suggest ways of modifying and extending teaching methods to help students develop mathematical thinking from their own ways of reasoning.

1. Proving in the curriculum

In North America three curricular positions regarding proving can be identified.  In some places proving is taught as part of geometry, the teaching of which occupies the second year of high school.  In other places the curriculum has been reorganized, downplaying geometry and proving.  This move may have been inspired in part by the poor results of teaching proving in geometry (Senk, 1985).  Other places have adopted the NCTM Standards (1989) as the basis for their curricula.  The Standards place considerable emphasis on mathematical reasoning in general, and proving in particular, and encourage the teaching of proving in all mathematical contexts, not just geometry.

Alberta

The current curriculum of Alberta illustrates the second curricular position, the downplaying of geometry and proving.  In the introductory material to both the Courses of Studies, and the Teacher Resource Manuals for grades 10, 11, and 12, the following definitions occur:

Throughout the learner expectations, the words verify and prove appear.  For the purposes of the Senior High Mathematics Program, they are interpreted as:

•     Verify:        to substantiate the validity of an operation, solution, formula or theorem through the use of examples that may or may not be generalized;

 

•     Prove:        to substantiate the validity of an operation, solution, formula or theorem in general and to provide logical arguments for each step in the process. (Alberta Education, 1991, p. 5; 1990, p. 6; 1989 p. 5; emphasis in original.)

Note that ‘proving’ refers only to deductive reasoning used to verify.  The use of ‘proving’ in this restricted sense is common in mathematics education.  Even though attention is paid to the definitions of these words, which are supposed to occur “throughout the learner expectations,” proving is rarely mentioned in these documents.

In the Program of Studies (Alberta Education, 1989) for Math 10^*, the word “verify” occurs six times in 102 pages.  “Prove” does not occur, but expectation 1.1.1 in the topic area Coordinate Geometry and Graphing reads: “Students will be expected to be able to deduce the distance formula from the Pythagorean theorem.”  This is the only explicit reference to proving in the Math 10 curriculum documents.

In the Course of Studies (Alberta Education, 1990)  for Math 20, “prove” does not occur; however, students are expected to provide two “logical arguments” in the context of geometry (pp. 12, 13).  The word “verify” occurs four times in that document. 

In Math 30, things improve somewhat, as proving is mentioned in non-geometric contexts.  Students are expected to prove the Remainder Theorem and the Factor Theorem in the unit on Polynomial functions (Alberta Education 1991 p. 37) and to prove trigonometric identities (p. 44). 

The discussion of the expectations related to proving in the Math 30 Teacher Resource Manual (Alberta Education, 1991) are interesting as an illustration of the ways proving is seen by curriculum planners.

Manipulating trigonometric identities provides an excellent opportunity for students to learn to “prove” that a given relationship is true.  The nature of proof should be discussed, particularly in terms of the difference between a verification using particular values of the variable and a complete argument that demonstrates truth in general.  A discussion of the nature of deductive and inductive proofs would fit well here....

Students should be encouraged to present logical arguments to show that the quotient and Pythagorean identities are true.  Note that this does not necessitate the use of the T proof processes that were so common in the teaching of deductive geometry.  This is an excellent place to discuss deduction and show students that a proof is a 

---

logical, cogent sequence of statements beginning with what is given or is known to be true, followed by statements based on previously established knowledge and concluding by what is to be proved.  (p. 45, quote marks in original)

The curriculum planners clearly see proving as a process whose function is verification.  Although the definition of “prove” they gave in the introductory material implied that proving is a deductive process, they imply here that “proofs” can be either deductive or inductive.  Proofs must also be semi-formal, hence the requirement that variables be used instead of specific values.  The second paragraph concentrates on the form of a proof.  The warning against “T” proofs reflects the practice of requiring such proofs in the past^* . 

It should be noted that even in a curriculum which pays scant attention to proving, mathematics is described as useful in developing logical reasoning.  Alberta Education’s “Program Rationale and Philosophy”, which appears in all the senior high school curriculum documents, states that: “an understanding of mathematical techniques or processes ... will enable [students] to ... acquire higher order skills in logical analysis and methods for making valid inferences.”  (Alberta Education, 1991, p. 1; 1990, p. 1; 1989, p. 1)

During my research studies I had the opportunity to see how three well respected teachers interpret the Alberta curriculum in their classroom.  Two of the three made no mention of proving to verify in the time I observed them.  The third, Ms E, described algebraic determinations of slopes of lines as “proofs”.  Examples of her teaching appear Chapter II, section 3.  In most cases mathematical statements made by the teacher were verified inductively by examples or by reference to the teacher’s knowledge and authority.

The Standards

The NCTM Curriculum and Evaluation Standards for School Mathematics (1989) reflect a different approach to proving.  Of the 14 standards for senior high school mathematics, standard 3 is “mathematics as reasoning”.  This is also one of the 13 standards listed for the lower grades.  The Standards document is a publication of North America’s largest mathematics education organization, which is intended to “guide reform in school mathematics in the next decade” (NCTM, 1989, p. v).  The inclusion of reasoning as one of the key standards in this document indicates the importance attached to proving in mathematics education. 

Standard 3 states:

In grades 9-12, the mathematics curriculum should include numerous and varied experiences that reinforce and extend logical reasoning skills so that all students can—

•     make and test conjectures;

•     formulate counterexamples;

•     follow logical arguments;

•     judge the validity of arguments;

•     construct simple valid arguments;

and so that, in addition, college-intending students can—

•     construct proofs for mathematical assertions, including indirect proofs and proofs by mathematical induction.  (p. 143)

The function of these reasoning skills that the NCTM envisages can be seen in their description of the practice of mathematics:

A mathematician or a student who is doing mathematics often makes a conjecture by generalizing from a pattern of observations made in particular cases (inductive reasoning) and then tests the conjecture by constructing either a logical verification or a counterexample (deductive reasoning)....Furthermore, all students, especially the college-intending, should learn that deductive reasoning is the method by which the validity of a mathematical assertion is finally established.  (p. 143)

This vision of proving is well within what Dawson (1969, p. 142) called the “naive heuristic of mathematical inquiry.”  Based on the work of Lakatos (1963/1976) Dawson identified a second heuristic, the deductive heuristic, in which the function of proving is to explore rather than to verify.  Proving to explore is described in detail in Chapter II.

2. Current practices in teaching proving

Proving has been a part of teaching mathematics since at least the time of Plato.  But millennia of experience does not mean teaching is as good as it can be.  In fact, the current methods fail to teach many students to prove (Senk, 1985; Schoenfeld, 1985; Fischbein, 1982).  What, then, is wrong with the way we teach?

People learn when they have a need which learning might fulfill.  As Vygotsky observed, learning is adaptation and it is a truism that “all adaptations are regulated by needs” (1986, p. 37)  There have been two needs that teachers by and large have invoked in order to motivate students to prove: the need to succeed in school and the need to know with certainty.

Of the three curricular approaches to proving mentioned in the previous section, the two most common are the teaching of proving in a year long course in Euclidean Geometry, and the downplaying of proving, as in the Alberta program of studies.  Schoenfeld (1985) describes teaching in the first of these contexts.  I will illustrate teaching in the Alberta context with observations from my studies in high schools (see Appendix B for descriptions of these studies).

Schoenfeld on teaching for examinations

At the school Schoenfeld studied, the teaching of proving involved a requirement that students prove propositions on a timed examination.  Schoenfeld traced the effects this requirement had on what teachers taught and what students believed.  Students were expected to prove one of a set of 30 propositions in Euclidean geometry on New York’s Regent’s examination. For Schoenfeld this expectation explained the adoption by their teacher of drill and memorization as his main teaching methods.  In this context the students became adept at the speedy production of precise constructions and at memorizing proofs.

 

In addition to encouraging memorization, Schoenfeld found that the examination system motivated the development of beliefs about the role of proving in mathematics.  The two beliefs Schoenfeld mentions which are most closely related to proving are these:

The processes of formal mathematics (e.g., “proof”) have little or nothing to do with discovery or invention.

Only geniuses are capable of discovering creating or really understanding mathematics.  (Schoenfeld, 1988, p. 151)

The antecedents of these beliefs in teaching probably include the practice of ignoring proving in the context of constructions and definitions, the other main topics of students’ work in Euclidean geometry.  The verification of constructions, which could be made an important context for proving, is often done visually — hence the stress observed by Schoenfeld on precision in constructions.  Definitions are usually presented as fait accompli rather than evolving from the needs of proving, as advocated by Borasi (1991).

The second belief noted by Schoenfeld, that mathematics is created only by geniuses, might also be related to the requirements of examinations.  Examinations require that a certain collection of facts, procedures, and skills be mastered.  This content is not organized as if it arose from a probable sequence of mathematical explorations, but rather as the endpoints of many explorations which have found application in some context deemed important at some time or another.  As a result a teacher allowing students to engage in any creation of mathematics would be doing them a disservice since it would detract from mastering the content required by the examinations.  Even if the content were such that a teacher could expect students to create it in the course of exploration, such a course would still be irresponsible since the course of exploration can never be entirely controlled, and the presence of digression can only serve to distract students from the required content.  Given the beliefs about math and the prevalence of memorized proofs encouraged by examinations it is not surprising that teaching based on using scholastic success to motivate students has failed to result in many students learning to prove.

Teaching at North and South Schools

The teaching of mathematics I observed at North School made no reference to proof or proving.  Verification of answers was done inductively or by reference to the authority of the teacher or textbook.  The focus was on learning procedures for obtaining answers quickly and accurately.   In the Math 13 class, this was a conscious decision of Mr. A, who felt the students would be best served by extensive practice of procedures without being confused by proofs.  In the Math 30 class Mr. B had made explanatory proving a part of his teaching, but the students, concerned with performance on their final examinations, had asked him to limit himself to what was going to be on the test. 

At South School, proving was identified with algebraic methods and was associated with verification.  On several occasions Ms E pointed out that a graphical rendering of a situation is not a proof and that proving required algebraic manipulations based on formulae.  On other occasions, while graphs were rejected as proofs, the only alternative offered was the authority of the teacher. 

 

3. Experiments in teaching proving

Fawcett (1938) suggests these assumptions as the basis of the teaching of proving:

1.   That a senior high school pupil has reasoned and reasoned accurately before he begins the study of demonstrative geometry.

2.   That he should have the opportunity to reason about the subject matter in his own way.

3.   That the logical processes which should guide the development of the work should be those of the pupil and not those of the teacher. (p. 21)

In Chapter I, section 2, I have indicated my reasons for believing that students can prove, in agreement with Fawcett’s first assumption.  His second and third assumptions could well have been listed by any present day proponent of the constructivist theory of learning.  In the following discussion of the teaching of proving I will be accepting Fawcett’s assumptions, as well as two more:

4.   The proving which is taught in mathematics should reflect the nature of proving in professional mathematics.

5.   The teaching of proving should take into consideration not only the form of proving used, but also the need which proving is satisfying in that context.

In my examination of the research literature on proof and proving, I have encountered only three studies of teaching in which proving was taught it a manner consistent with Fawcett’s assumptions.  These studies are those by Fawcett himself, Balacheff and his coworkers (Balacheff, 1991;  Arsac, Balacheff, & Mante, 1992) and Lampert (1990).  I would like now to describe the work of these researchers and to comment on them in light of assumptions #4 and #5.

Fawcett’s research

Fawcett’s research is the subject of an NCTM Yearbook (Fawcett, 1938).  In it he describes in detail his methods of teaching and the results he obtained, according to both interviews with students and standardized tests.  In general he was quite successful and it is not clear why his straightforward suggestions for improving teaching were not implemented more widely.  His description of the teaching methods he hoped to replace are quite similar to those described by Schoenfeld (1985) which I related in the previous section. 

In some respects Fawcett’s teaching seems quite traditional.  He makes no reference to students working together, except in the context of whole class discussions led by the teacher.  The context for teaching proving is geometry and although Fawcett does note the importance of students being able to transfer their ability to prove to non-mathematical domains, he does not discuss proving in other areas of mathematics.  Other aspects of his teaching are fairly radical, at least compared to current practice.  He summarizes his methods as follows:

 

1.   No formal text is used.  Each pupil writes his own text as the work develops and is able to express his own individuality in 

 

organization, in arrangement, in clarity of presentation and in the kind and number of implications established.

2.   The statement of what is to be proved is not given the pupil.  Certain properties of a figure are assumed and the pupil is given an opportunity to discover the implications of these assumed properties.

3.   No generalized statement is made before the pupil has had an opportunity to think about the particular properties assumed.  This generalization is made by the pupil after he has discovered it.

4.   Through the assumptions made the attention of all pupils is directed toward the discovery of a few theorems which seem important to the teacher. 

5.   Assumptions leading to theorems that are relatively unimportant are suggested in mimeographed material which is available to all pupils but not required of any.

6.   The major emphasis is not on the statement proved, but rather on the method of proof.

7.   The extent to which pupils profit from the guidance of the teacher varies with the pupil and the supervised study periods are particularly helpful in making it possible to care for these variations. In addition individual conferences are planned when advisable. (p. 62, emphasis in original)

Fawcett was quite successful in achieving the objectives he set for himself.  His teaching cannot be criticized on the basis that it does not work.  In fact, in many ways his methods seem deserving of application in the teaching of mathematics in general, not just proving.  At the same time I have some concerns related specifically to the aims of his teaching.  Fawcett assumes that the purpose of proving is the determination of truth.  He makes no reference to proving as explaining or exploring although the students in his course did a fair bit of both.  He is also concerned that his students be able to transfer their ability to prove to “non-mathematical material” (p. 21).  In his classes the non-mathematical material examined consisted of advertisements, political arguments, and legislation.  He achieved some success in persuading his students to reason deductively outside of mathematical contexts, as indicated by these comments he received from parents by way of another teacher who conducted interviews with them:

The parents fear that the course may tend to inhibit in the boy the power of imagination for creative writing in English.  For example, when he was writing of a personal experience for an English assignment he resented some suggestions his mother made in order to add interest to the composition on the basis that the suggestions were not facts.  He wished to write only in a scientific manner.

The mother fears that the girl may carry her criticism to the point of quibbling, however.  In some cases she has gone to the point of criticising authorities on subjects about which she knew nothing. (p. 109)

My point in quoting these comments is to suggest that presenting proving as verifying, and then encouraging students to employ proving in a wide range of contexts, could lead them to apply proving in cases where it is inappropriate and also to miss occasions when proving might be used to explain or explore but not to 

verify.  In the next chapter I have some further comments on the misapplication of proving to verify outside of mathematics.

Research by Balacheff et al.

An example of the studies being done in France by Balacheff and others is the study done by Arsac, Balacheff, & Mante (1992).  Students were presented with this task:

Write for other students a message allowing them to come to know the perimeter of any triangle a piece of which is missing.  To do so, your colleagues will have at disposal only the paper on which is drawn a triangle and the same instruments as you have (rulers, etc.) (pp. 10-11)

The lesson was divided into two phases.  In the first phase the students solved the problem, working in groups. 

During the second phase, called the debate period, aiming at a collective discussion about the proposed solutions, the organization is the following:  Students’ solutions are written on a large sheet of paper and are then displayed as posters on the wall of the classroom.  Each team has to analyze the posters and their spokes-person tells the class their criticism and suggestions.  The criticism must be accepted by the team whose poster is discussed.  Since the students involved are 13 to 14 years old, it is not possible to leave them free of any regulation.  The management of the activity is then left to the teacher.... The social situation, as a whole, constitutes here the didactical milieu of the students’ mathematical activity.  But such a milieu is not sufficient by itself to guarantee the quality of the debate.  We can then foresee that the teacher will have to play a role especially when the student group might come to an incorrect agreement or to an impasse. (p. 9, emphasis in original)

I liken this process of presentation of arguments followed by consensus decision making to a judicial trial, with the students acting as both lawyers presenting arguments and as jurors evaluating the argument.  The teacher plays the role of the judge, advising the jury on the admissibility of evidence.  Teaching based on this “courtroom” metaphor has much to recommend it .  The body of mathematical knowledge provides a codified basis for argument, much as the body of laws provides a basis for legal arguments, especially in legal systems based on the Napoleonic code, such as France and the United States.  In addition, the process of evaluating major mathematical propositions within the mathematical community has characteristics of a legal proceeding.  The evidence for a proposition, a proof, is offered to the community, experts comment on it and point out flaws.  These are then corrected, and perhaps new arguments are brought forth, until finally the proposition is accepted into the body of mathematical knowledge.

The research done on the basis of the courtroom model also places a strong emphasis on communication.  This is important as an encouragement to formulate unformulated proving.  This practice could help students to overcome the difficulty in formulating I observed in my studies. 

Research by Lampert in the United States

Lampert (1990) has taken the important steps of attempting to teach proving to students in the early grades.  She taught a grade 5 class using a method similar to that employed in France, with modifications appropriate to younger students.  

As students volunteered their solutions to a given problem, I write them on the board for consideration, and I put a question mark next to all of them....  Once the list of students’ solutions was up on the board, they were open for discussion and revision....  If they wanted to disagree with an answer that was up on the board, the language that I have taught them to use is, “I want to question so-and-so’s hypothesis.” ... I always ask them to give reasons why they questioned the hypothesis, so that their challenge took the form of a logical refutation rather than a judgment. (p. 40)

Lampert also placed some emphasis on portraying mathematics as exploratory, in keeping with Lakatos’ (1976) historical analysis (see Chapter I, section 2).  She is especially aware of the “cultural” side of teaching proving:

I assumed that changing students’ ideas about what it means to know and do mathematics was in part a matter of creating a social situation that worked according to rules different from those that ordinarily pertain in classrooms, and in part respectfully challenging their assumptions about what knowing mathematics entails. (p. 58)

Teaching based on the “courtroom” metaphor provides a context for the development of a culture of proving.  The importance of such an atmosphere is indicated in the encouragement to prove it provided the participants in my studies. 

Weaknesses of teaching based on the courtroom metaphor

Teaching based on the courtroom metaphor does have some shortcomings.  One of these is pointed out by Arsac, Balacheff, & Mante (1992), who report that in classrooms the arguments offered are often not entirely founded on mathematical bases, but include appeals to social and personal factors.  Students rely on their personal authority as members of the social structure of the class to verify their statements by reference to their own authority.  This is entirely in keeping with the metaphor since the decisions of juries are as much determined by the persuasive abilities of lawyers as they are based on the code of law. 

A second flaw in the courtroom metaphor is found in the need a trial serves: the establishing the truth or falsity of charges.  A legal proceeding verifies.  In the same way teaching based on the courtroom metaphor verifies the conjectures that students make.  As I noted above, professional methematicians use proving to satisfy needs other than verifying, and the results of my studies indicate that proving to verify is contrary to students’ inclinations.  It is the stress on proving to verify which is, in my mind, the major problem with the courtroom approach to teaching proving.

4. Speculations on improving teaching

The research on teaching proving I have described above contains many excellent suggestions for improving teaching, which I can only reiterate.  There are shortcomings in the basic assumptions of these efforts, however.  Chief among these is that the need to prove is a need to verify.  I believe that the teaching of proving ought to center on the importance of proving as a way of explaining and exploring in mathematics and also in the sciences and in dealing with a technological world.

Teaching with this aim must still include several of the important features of Fawcett’s teaching, and of teaching in the courtroom metaphor.  These features are the following:

 

1.   Providing situations for proving in which results are discovered by the students, and in which the need to prove arises out of a need to explore, explain, or verify in the situation.

2.   Statements which are proved are proposed by students, at the level of precision the students find necessary.

3.   The need to define precisely arises out of the requirements of proving, not as an arbitrary imposition by authority.

4.   “The major emphasis is not on the statement proved, but rather on the method of proof” (Fawcett, 1938, p. 62, emphasis in original)

5.   Providing occasions for students to express their reasoning in their own way, and in ways which permit communication with their peers and with the larger mathematical community.

6.   Proving occurs in a social context in which there is an expectation that explanations will be deductive and in which accommodation is made for the time and attention explaining by proving requires.

In addition to these principles, I would propose an alternative to the courtroom metaphor implicitly used by Lampert, and Balacheff, et al.  Inspired by the deductive methods of Sherlock Holmes and by the mathematical acumen of his nemesis, Prof. Moriarty, I would propose a metaphor of mathematics as detective work.  This metaphor shares important features with the courtroom metaphor like communication and the fostering of a “culture of proving.”  At the same time it emphasizes the importance of proving as a way of explaining and exploring in mathematics and provides a basis for exploration by formulated proving by inviting the question, “What do you know?  What clues do you have?”

A small shift in emphasis can bring teaching based on the courtroom metaphor closer to the detective metaphor.  In the courtroom the objective of the lawyers’ arguments is to convince the jury.  A detective is more concerned with proving to explain than to convince, and this suggests some changes to the teaching methods of the courtroom metaphor.  The same process of generating conjectures occurs, but instead of the students attempting to convince each other, they attempt to explain to each other. They try to help the other students understand why their conjecture is true, not just that it is true.  This shift in focus builds on the use of proving to explain which was indicated in my studies, and in previous research (Hanna, 1989; de Villiers, 1991).  It also makes the decision process less one of conflict and more one of consensus building.

A more complete development of the detective metaphor involves the students in significant investigations in mathematics.  Such investigations require complex and open situations, teacher support and guidance, and a culture of proving in the classroom, such as some of those suggested by Fawcett (1938).

The problem prompts employed in my research begin to suggest the sorts of situations which would permit mathematical investigations involving proving.  They could be criticized on the basis of being unconnected to the topics in many high school curricula.  I consider this less of a difficulty than the limited scope of the problems.  The Fibonacci situation can be expanded to include other topics (e.g., the golden mean) but it is practically limited to the properties of the sequence itself.  The Arithmagon situation can include a wide range of uses of systems of equations and linear algebra, but at the same time it imposes constraints on the interpretations of these topics.

I would propose that the best problem prompts might already appear in our textbooks, either as mathematical problems which involve most of the content of a unit, or as “add-on” or “enrichment” activities linking the content with genuine applications of mathematics in business, science, or the arts.  For example, the problems Ms E presented at the end of her unit on equations of lines involved finding equations of altitudes, medians, and perpendicular bisectors of the sides of triangles.  These problems could have been presented at the beginning of the unit as  problems for investigation.  Determining the point of intersection for these lines could have extended the same problems into the next unit on linear systems.

Fawcett (1938) provides other examples of good problems for investigation:

Referring to the diagram [Figure 32] let us assume that AP and AQ are tangents drawn to circle O from an external point, A.  What are the implications of this assumption?

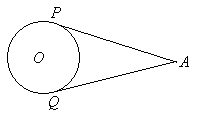
Figure 32: Fawcett’s diagram.

Draw a right triangle and from the vertex of the right angle draw a perpendicular to the hypotenuse.  What properties of this figure can you discover and establish by deductive proof? (p. 91)

I would replace the phrase “establish by deductive proof,” in Fawcett’s second problem with the word “prove” but otherwise these problems seem to be excellent starting points for mathematical investigations.  Fawcett’s students’ investigations led them to a wide range of discoveries, including the Pythagorean Theorem, which is suggested by the second problem. 

To contrast the results of current teaching methods with what could occur if students spent more time proving to investigate problems like these, consider the behavior of students interviewed by Schoenfeld (1985).  When given the diagram 

in Figure 33 and asked to prove that PA @ QA and OA bisects PAQ the students could do so easily.  When given the same diagram with the circle omitted a few minutes later, and asked to construct a circle tangent to PA at P and also tangent to PQ, they attempted to do so by constructing various arcs and lines with the inaccurate compass Schoenfeld provided, judging whether they had succeeded by the appearance of the result.  No attempt to use the proving they had done previously was made.  Would students who had learned to prove to explore, not just to verify, have behaved the same way?

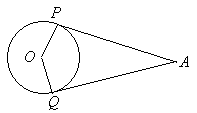
Figure 33: Perpendiculars to tangents meet at the center.

Throughout such investigations the teacher plays vital roles, as observer, guide, resource, and co-investigator.  These roles focus the teacher on the process of doing mathematics, on reasoning and understanding, and on the mathematical worlds of the students.  They stand in contrast with more traditional teacher roles as an authority on mathematical knowledge and the active agent in the classroom.

As an observer the teacher assesses the reasoning and understanding of students so as to be better able to guide them in their investigations.  This role also plays an important part in the investigation itself since an observer can record and recollect parts of the investigation which might be useful later.  This recollection is also an aspect of the teacher’s role as a resource.  In acting as an observer, the teacher is modeling an activity which the students themselves should learn as part of mathematical and scientific investigation. The role of observer might be usefully assigned to students as one way of contributing to a group investigation.

Guiding students should not be confused with “funneling” them towards a known goal along a familiar path.  Guiding students’ investigations is more concerned with pointing out important signs, reflecting on reasoning, raising unthought of possibilities and, on occasion, warning students away from unprofitable paths.  It must be emphasized that investigation is not about efficiency and optimization.  In every path there is some value.  The teacher does have a responsibility, however, to proscribe the range of investigation to exclude paths which are known to be generally unproductive, or even misleading.

In addition to recalling students’ recent actions and discoveries, the teacher is also a source of information and ideas.  Of course, this is a large part of teachers’ traditional role but with an important difference.  While the usual pattern is for teachers to anticipate what skills and knowledge students’ will need (as Ms E did in her unit on graphing lines), a teacher acting as a resource for an investigation must learn to wait and listen and to provide students with information when it is needed, not before.  This was the role my co-researchers and I adopted in problem sessions.  While we asked questions to point out aspects of the situation for the participants to continue their investigations, we gave answers only to the participants’ own direct questions.  Interestingly, those participants who were most willing to ask questions asked only to allow themselves to continue investigating without the impediment of 

stopping to make calculations.  They asked no questions that would dispel the mystery they were investigating.

The openness of the problem prompts used in my research created situations in which the participants knew as much about what was going on as the observers did.  This was especially true in the Arithmagon situation, in which almost all the participants, including both the first and the last groups observed, surprised me with aspects of the situation I had not anticipated.  Classroom investigations should also afford the opportunity for teachers to join their students in genuine mathematical activity, complete with the uncertainty of exploration.  This places a demand on teachers unlike those often encountered.  What is most important for teaching in investigations is a willingness to learn and to live with the uncertainty which come with learning.

Permitting the development of a culture of proving in a classroom is a difficult task.  Some studies (e.g., Perry, 1981; Belenky, Clinchy, Goldberger & Tarule, 1986) suggest that students are not prepared to participate in such a culture prior to their university education, or that current schooling practices delay the development of the necessary attitudes towards knowledge until students enter universities.  Lampert (1990) offers some hope that the real situation is the latter.  She reports success in developing in grade 4 and grade 5 students attitudes appropriate to mathematical investigations.  These attitudes are described by Polya (1968) as “intellectual courage,” “intellectual honesty,” and “wise restraint.”

 

First, we should be ready to revise any one of our beliefs.

Second, we should change a belief when there is a compelling reason to change it ...

Third, we should not change a belief wantonly, without some good reason.  (p. 8)

In addition to these attitudes, classrooms also need to present opportunities for mathematical discourse, such as are described in the NCTM Professional Standards for Teaching Mathematics  (1991, see also Reid, 1994).

In order for students to develop the ability to formulate problems, to explore conjecture and reason logically, to evaluate whether something makes sense, classroom discourse must be founded on mathematical evidence.

Students must talk, with one another as well as in response to the teacher.  When the teacher talks most, the flow of ideas and knowledge is primarily from teacher to students.  When students make public conjectures and reason with others about mathematics, ideas and knowledge are developed collaboratively, revealing mathematics as constructed by human beings within an intellectual community.  (p. 34)

5. Why teach proving?

You will have noticed that the critiques of the teaching methods proposed by Fawcett, Balacheff, and Lampert (above), could as easily be applied to the curricular objectives I described at the beginning of this chapter.  The justification given for teaching proving is that proving is the way to verify in mathematics.  If I 

argue that this justification misrepresents mathematics and proving, and leads to teaching in ways which neglect students’ needs to prove, what then is the reason to teach proving at all?

Perhaps the best way to begin to answer this question is to look at the reason we teach anything.  Bruner sums it up nicely:

A culture is as much a forum for negotiating and renegotiating meaning and for explicating action as it is a set of rules or specifications for actions.  Indeed, every culture maintains specialized institutions or occasions for intensifying this ‘forum-like’ feature. Storytelling, theatre, science, even jurisprudence are all techniques for intensifying this function—ways of exploring possible worlds out of the context of immediate need. Education is (or should be) one of the principle forums for performing this function—though it is often timid in doing so.  It is the forum aspect of a culture that gives its participants a role in constantly making and remaking the culture.  (Bruner, 1986, p. 123, emphasis in original)

According to Bruner, and I would have to agree with him, education has two aims.  The first is simple.  We want to pass on aspects of our culture which we consider to be important to our children.  In doing so we are presenting them with “a set of rules or specifications for actions” which will allow them to continue to be a part of a world defined by our culture.  For this reason we teach children to speak the language we speak, to listen to music like the music we listen to, to read books we have read, and to appreciate the dramatic arts as much as we do.

Passing on our culture to students takes many forms, from providing basic skills and knowledge we know all of them will need, to exposing them to the more esoteric aspects of human culture, giving them opportunities to go where they might otherwise never have ventured.  Among the basic skills of living in our society is an ability to reason deductively as a basis for problem solving in encounters with technology and as a tool for evaluating scientific, legal, and statistical arguments used to justify public policy.  Proving is also an introduction to the esoteria of mathematics, physics, and analytic philosophy, which are as much a part of our culture as the poems of Milton and the music of Bach, and so as important to students’ education.

It is vital not to be confused about the importance of basic skills versus exposure to esoteria.  Teaching students the relevance of proving to mathematics or philosophy is not the most central of our aims and teaching needs to reflect this.  Reasoning deductively to determine the functions of, or flaws in, a product of rational design science is a more central aim.  This should be apparent in the contexts for reasoning we choose for our students.  Students may learn to prove as well in thinking about set theory as in thinking about microwave oven programming, but the reasons to prove communicated will be quite different.

The second aim of education, according to Bruner, is to give students “a role in constantly making and remaking the culture.”  Deductive reasoning is an important part of our culture and a part of our culture in need of being remade (as I discuss further in the next chapter).  An important part of remaking this part of our culture is detecting misuses of proving.  In some cases these become apparent from the unsatisfactory results obtained, but it is better to notice misuses of proving before they cause harm, and in a way which includes an understanding of the

weaknesses which make proving unsuitable for a particular use.  The ability to do this depends on an ability to prove.

The misuse of proving might be a result of flawed proving, or it might result from the use of proving in an inappropriate context.  When the misuse of proving is a result of errors in the proving process it is only through proving that the errors can be discovered.  This use of proving might be compared with Lakatos’ “proving to improve” (1976, p. 37) in mathematics, broadened to include proving in other contexts.  When a correct proving process is used in an unsuitable context, proving provides the basis for a precise understanding of its own limits. 

The use of proving in our culture, its misuses in inappropriate contexts, and the ways in which proving can define its own limits, are the topic of the next chapter.