APPENDIX E
METHODS OF SOLUTION
While the methods the participants used to solve the initial puzzles and the generalizations they made in the problem situations were not objects of my studies, they are of sufficient interest to warrant their inclusion here. They may serve to provide those readers who have not had time to investigate the problem situations themselves an opportunity to see the openness and possibility of the problems.
1. Arithmagon
The numbers on the sides of this triangle are the sums of the numbers at the corners. Find the secret numbers.

Figure 35: The Arithmagon prompt.
Most of the participants were given a problem prompt containing nothing but the initial puzzle shown in Figure 35 and the cryptic instruction to “Generalize the problem and its solution.” In the following sections I will describe, in turn, specific solutions to the puzzle, general solutions, and general problems.
Specific solutions to the puzzle
I have seen three solutions to the puzzle which I do not consider to be general solutions, for various reasons. The constraints method involves an assumption which is not generally true, so that while it does solve the given puzzle, it cannot solve all puzzles. Using a system of equations is quite general, in fact too general, and it tells us nothing about the Arithmagon itself. If it is solved for the general case with three variables on the sides, I consider the resulting formula to be a general solution to the Arithmagon. If every Arithmagon requires solving a new system, however, that is not general enough for me. The method of false position is quite general, but the one person I have seen come up with it did not see it that way, so I include it here as a specific method.
The constraints method
This method was used by about half the participants. It is based on an assumption that the secret numbers are whole numbers, which they are in the case of the initial puzzle, so they can be found this way. The method is an intelligent
guess and check. Ben described this method to Rachel, Eleanor, and Wayne as the way he had solved the puzzle (see Chapter II, section 1).
The assumption that the secret numbers are whole numbers means they cannot be less than 1. How large they can be depends on the numbers on the sides. The secret number at the top can be at most 10, because it must add to another number, which we know is at least 1, to give 11. Similar reasoning gives maximum values for all the secret numbers. It is now a simple matter of trying all the values in the allowed range of one secret number until we find the right one. If we start with the value 1 for the top number (which most participants did) we quickly find that the secret numbers are 1, 17, 10.
Systems of equations
If we label the diagram as shown in Figure 36 we can express the relationships between the secret numbers A, B, C, and the number on the sides in these three equations:
(1) A + B = 18
(2) B + C = 27
(3) C + A = 11
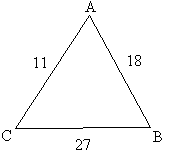
Figure 36: Labeling the Arithmagon for a system of equations.
Subtracting equation (1) from equation (2) yields: (4) C – A = 9
Adding equation (4) to equation (3) yields: (5) 2C = 20
Dividing by 2 yields: C =10. The remaining values can be found by substituting 10 into the equations wherever C occurs, or by writing in 10 on the diagram and working around the triangle, subtracting to find the unknown numbers.
The method of false position
One solution which none of the participants used, but which I have seen in another context, is similar to a historical technique for solving equations known as the method of false position. Begin with a corner, say the top, and pick a number, say 5. If the top were 5 then the lower left would be 6, and the lower right would be 13. The sum of these is only 19, so they are too small. That means our original guess was too big. We might simply try reducing it by some amount at random, and we would quickly zero in on the right value. However, we can be a little bit more clever. Our sum for the base was wrong by 8. Changing the top number makes changes in each of the bottom corners equally, so it makes sense that an
answer which is too low by 8 means that each of the bottom corners is too low by 4. So the lower left is 6+4 = 10 and the lower right is 13+4 =17.
General solutions
The usual formula
As I noted above, solving the Arithmagon using a system of equations with variables in place of the known side numbers yields a general formula, A = , where x is the side opposite the secret number A. Expressed verbally, it is “Add the two adjacent sides and subtract the opposite one.” This formula was also discovered inductively by some participants, and by proving in the case of Sandy (see Chapter II, section 2).
Stacey and Kerry’s method
This method is quite unusual, and based on the extended explorations undertaken by Kerry and Stacey. It is described in Chapter III. I will repeat the gist of it here.
Begin by drawing another triangle around the original triangle (see Figure 37). Add the known numbers and divide by 4 (in this case we get 56÷4=14). Subtract this number from each of the known sides, and write the values you get on the corners of the new, larger, triangle (see Figure 37).
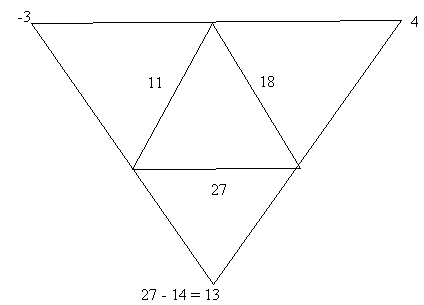
Figure 37: Stacey and Kerry’ general solution.
Adding these values in pairs, (e.g., 13+4 =17) gives the side numbers for the larger triangle, which are the secret corner numbers for the original triangle. It really works! If you will not take my word for it (verifying by authority) try it a few times (verifying inductively) or see the proof in Chapter III (verifying by proving).
Colin and Anton’s method
Colin and Anton noticed that the difference of two corner numbers is the same as the difference of the numbers on the two sides they do not have in common. (see Figure 38). They discovered this relationship inductively and later explained it deductively (See Chapter II, section 1). Once this relationship is known it establishes enough information to quickly find an answer. For example, in the original triangle, it tells us the difference of the secret numbers on the base is 18‑11 = 7 (Notice that the equation C – A = 9 which came up in the solution using system of equations expresses the same relationship for two other secret numbers). We know their sum is 27 and their difference is 7. Anton would usually find the numbers quickly by guess and check at this point, but on one occasion Colin suggested subtracting the difference from the sum to find twice one of the numbers, and then dividing by 2. They had a great deal of difficulty formulating this method, but had they succeeded it would have produced a formula like A = , which is similar to the “usual” formula, though it reveals its much different origins.

Figure 38: Colin and Anton’s difference relation.
Eleanor’s method
Working with Ben and Wayne, Eleanor notice two important relationships between the numbers in the Arithmagon. They are: a+z = b+y = c+x and a+b+c = 2(x+y+z) (see Figure 39).

Figure 39: Labeling of triangle for the basic relations in Eleanor’s method.
Using this relation she developed a general method for solving the Arithmagon. Her method begins by adding up the known numbers, and dividing
by 2 (yielding 27 in the original puzzle). She then writes this in the center of the triangle (see Figure 40). Subtracting each of the known sides from this number yields the secret number on the corner across from it.
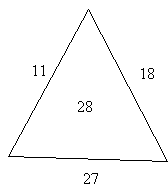
Figure 40: Eleanor’s “middle” number.
General problems
The Arithmagon problem can be generalized in several ways. Generalizations of the problem did not occur spontaneously to any of the participants. The idea of Arithmagon squares was suggested to several groups (and included in the prompt used at North School), and some investigations of Arithmagon squares did occur. Stacey and Kerry were the only participants to look at Arithmagons of more than four sides.
Other than generalizing the number of sides of the Arithmagon, one can also generalize to higher dimensions, and investigate Arithmagon polyhedra (Arithmahedra?), or, in the abstract, figures of 4 or more dimensions. Or one could look at the effect of using the product or difference of the two secret numbers to produce the numbers on the sides.
2. Fibonacci
The Fibonacci sequence begins:
1, 1, 2, ...
and continues according to the rule that each term is the sum of the previous two (e.g., 1+1=2).
The Fibonacci sequence has many interesting properties.
Can you find an interesting property of every third Fibonacci number?
Can you find other interesting properties?
Figure 41: The Fibonacci prompt.
The investigation of the Fibonacci sequence usually turned into a property hunt. All this hunting did result in the discovery of some interesting properties. In
addition some participants generalized the sequence by loosening some of the requirements of its definition.
Properties of every nth Fibonacci number
Most groups noticed that every third Fibonacci number is even, but in many cases this was not considered interesting enough to be a property. In general every nth Fibonacci number is a multiple of Fn, so F3m is even because F3 is 2. Some participants, after noting the evenness property went on to notice the relation F3m = 4F3m-3 + F3m-6. For example F9=34, F6=8, and F3=2, and 34 = 4 ¥ 8 + 2. Similar relations hold for F4m, F5m, etc. with the multiplier ‘4’ being replaced by increasing terms of the Lucas sequence, 4, 7, 11, 18, ... Several groups noticed that Fibonacci numbers with prime indexes (Fp where p is prime) are also prime. No group noticed that this property fails for F19.
Generalizations of the Fibonacci sequence
Stacey and Kerry were the most enthusiastic generalizers of the Fibonacci sequence, but others also explored some of the possibilities. The sequence can be generalized by changing the initial values, changing the range the sequence is defined on, or changing the rule. No one tried changing the rule, perhaps because it is the most unusual aspect of the sequence. Stacey and Kerry examined the sequence without constraining the values to positive integers. They developed the integer sequence ... -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, ... They, along with other groups, also explored sequences beginning with values other than 1, 1.