previous table of contents next
APPENDIX B
DESIGN AND DÉROULEMENT OF THE RESEARCH STUDIES
The empirical basis of my research includes four research studies, and several isolated observations and interviews. The basic structure of each study was the same. Typically, a pair of students was observed in two problem solving situations, and then interviewed. Each problem solving session and the interview took about one hour and the sessions were spaced one week apart. Differences from this typical outline will be indicated below for each of the studies.
1. The North School study
Context
The study took place over a seven week period in the spring of 1994. The site was a large urban high school, which will be referred to as North School. The classes involved were both normally taught by the same teacher (called Mr. B here), but the period of the study overlapped the last four weeks of a student teacher’s practicum in Mr. B’s classes. This student teacher (called Mr. A here) had sole responsibility for teaching one of the classes chosen for observation. Mr. B taught the other class. Both teachers are highly competent. Mr. A’s lack of experience was compensated for by his enthusiasm and knowledge of mathematics and teaching methods. Mr. B. is a highly respected teacher both in his school district and in the community at large.
The classes chosen were selected to be as different as
possible in the high school context. One
class was a non-academic 10th grade class (Math 13), which was taught by Mr.
A. It had a total enrollment of
nearly 30, but normal attendance ranged between 20 and 25.
The other was a 12th grade class for university bound students (Math
30). It had an enrollment of just
over 20, almost all of which were present every day.
Each class met three times a week, for 65 minutes each session.
Outline
The study was conducted in two phases, a classroom observation phase, and a small group phase.
In the first phase each class was observed engaged in their normal mathematical activities, over a period of three weeks. In this period field notes were kept of the general character of the classes’ activities, to provide context, and of particular observations of deductive reasoning employed by the students in the course of their normal activities. On some occasions audio tapes were made of class sessions which were then used to expand the records in the field notes.
In the second phase a pair of students who volunteered from each class engaged in problem solving activities. There were four sessions in this phase: two problem sessions, and two interviews. Each session was video taped for later analysis. During the problem sessions the students worked together on a single problem for about one hour. The researcher observed, interacting with the students only when they asked questions. During the interview sessions the researcher
asked the students about particular aspects of their problem solving, making use of video tapes of the problem sessions where appropriate. The students were also asked to continue work on the problems they had been given in the problem sessions, and to solve a new problem, with some help from the researcher. They were then assisted in making formal the reasoning they had employed in solving the problems. The problem situations used in the problem sessions were the Arithmagon and Fibonacci. The prompts for these problems are shown below (in section 7).
Participants
The students who participated in the second phase were selected from their classes on the basis of their willingness to participate, their involvement in class, and the reasoning they displayed in class.
The pair chosen from the Math 13 class I have called Bill and John. Bill sat behind John in class. At the time of the study Bill was doing very well in Math 13. He was normally attentive in class, and appeared to catch on quickly to the concepts presented to him. On two occasions, when Mr. A was absent and Mr. B was teaching the class, Bill responded at length to requests for explanations and alternative methods. Bill normally worked on seat work by himself. John had more difficulty than Bill, but was still able to succeed on most of the work required in the class. He rarely spoke in class, and worked by himself, except for rare occasions when he would consult with Bill on seat work with which he was having difficulty. On one of the uncommon occasions when John asked a question, he had noticed an unusual pattern in a linear equation, and wondered if it were general. (Briefly, John noticed that the solution, , of the equation 2 = + b, could be obtained by calculating 2 ¥ 7 = 14, and then subtracting 14 - 3 = 11, and placing this result over the denominator 7.)
The pair from the Math 30 class I have called Colin and Anton. They often worked together, or with others in the group of students sitting near them. Colin was the top student in his class. He was attentive, did all assigned work, and understood new concepts quickly. Anton was in the top half of the class, was less enthusiastic about doing seat work, and often needed to ask Colin or someone else to explain the procedures required by the assigned tasks. This was more due to his lack of attention to Mr. B’s explanations and instructions than to difficulties in comprehension. Anton was more talkative in class than Colin, although much of his talking was not related to mathematics.
2. The South School study
Context
The study at South School took place in the fall of 1994. South School is a large urban high school. One class was observed, taught by Ms E. Ms E is a highly competent and well respected teacher, who has made considerable efforts to promote mathematics at South School and through professional organizations. The class chosen was an “Academic Challenge” grade 10 (Math 10 AC) class. The students had been selected from among the most successful students in their grade 9 programs. The class met every day, for 80 minutes each session.
Outline
The general outline of the study was the same as for the North School study. The class was observed for two weeks, and then students were observed and interviewed. In the small group phase four groups of students participated. There were three sessions with each group, two problem sessions and an interview. Each session was video taped for later analysis. In keeping with the enactive methodology (described in Chapter VII) several researchers were involved in each session. Researcher interventions in the problem sessions were limited to answering the participants’ questions, and asking questions designed to encourage further investigations. During the interview session the researchers asked the participants about particular aspects of their problem solving, and proposed additional problems. The Arithmagon and GEOworld situations were used in the problem sessions (see below for prompts).
Participants
The students who participated in the problem sessions and interviews were selected from their classes on the basis of their willingness to participate, their involvement in class, and the reasoning they displayed in class. In general all the students did well in class.
Group I included three female students, Ann, Lynda, and Joanna. Ann was active in the class, asking and answering questions, and working with the students around her, including Lynda, who sat in front of her. Lynda was quiet, and participated in class only in her interactions with Ann. Joanna was active primarily in responding to Ms E’s questions, and working with the students who sat around her.
Group II included two female students, Tara and Topaz. Tara was active in working with the students around her, and in answering questions. Topaz was occasionally absent, and her main involvement in the class was working with the students around her and asking Ms E questions.
Group III include three male students, Joseph, Stephen and Scott. The three of them sat together, and often worked together. Scott was interesting in that he often talked to himself while working, and seemed quite involved in his work.
Group IV included two male students, Alec and Darrell. They normally worked by themselves, occasionally interacting with those around them.
3. The first clinical study
Context and outline
Two of the main studies were conducted with undergraduate students. These studies will be referred to as the ‘clinical studies’. The first clinical study occurred in the fall of 1993.
The clinical studies involved three problem solving sessions, followed by an interview. The problem situations used were the Arithmagon, Fibonacci, and GEOworld. In the first session each pair of participants worked separately on either the Arithmagon or the Fibonacci situation. In the second week each pair
worked in GEOworld. In the third week each pair worked in the situation they had not yet seen. The prompts used are given below, in section 7. For the sessions in the second and third weeks the pairs were grouped in two sets. Each set worked in the same situation at the same time, and could communicate with the other pair in the set. The situations and sets are summarized in Table 4. Each pair was interviewed separately in the fourth week.
|
Pair |
Week 1 |
Week 2 (set) |
Week 3 (set) |
|
I (B&W) |
Fibonacci |
GEOworld (A) |
Arithmagon (A) |
|
II (S&K) |
Arithmagon |
GEOworld (B) |
Fibonacci (B) |
|
III (E&R) |
Fibonacci |
GEOworld (B) |
Arithmagon (A) |
|
IV (J&C) |
Arithmagon |
GEOworld (A) |
Fibonacci (B) |
Table 4: Schedule of the sessions for the first clinical study.
Participants
The students who participated (with one exception, Kerry) were volunteers from a pre-service mathematics teacher education course. A total of eight students participated. The participants worked in the following pairs:
Pair I: Ben and Wayne. Ben and Wayne volunteered as a pair. Each of them had completed the mathematics requirements of the B. Ed. degree.
Pair II: Stacey and Kerry. When she volunteered Stacey asked to work with her friend Kerry. Kerry was student in Finance, and had completed courses in linear algebra and calculus as part of his degree. Stacey had completed the mathematics requirements of the B. Ed. degree.
Pair III: Eleanor and Rachel. Eleanor and Rachel volunteered separately and were paired by default. Eleanor had completed a bachelor’s degree in mathematics 15 years previously, which provided her with the mathematics entrance requirements for the B. Ed. degree. Rachel had completed the mathematics courses required as part of the B. Ed. degree.
Pair IV: Jane and Chris. Jane and Chris volunteered as a pair. They had both completed bachelor’s degrees in the past which provided them with the mathematics entrance requirements for the B. Ed. degree. Chris had recently completed a physics degree. Jane had completed a mathematics degree.
4. The second clinical study
The second clinical study took place in the fall of 1994. The context and general outline was identical to that of the first clinical study, except that the pairs never worked as a set of four. The schedule of sessions is summarized in Table 5.
|
Pair |
Week 1 |
Week 2 |
Week 3 |
|
I (J&T) |
Fibonacci |
GEOworld |
Arithmagon |
|
II (M&R) |
Arithmagon |
GEOworld |
Fibonacci |
|
III (L&D) |
Fibonacci |
GEOworld |
Arithmagon |
Table 5: Schedule of sessions for the second clinical study.
Participants
As with the first clinical study, the students who participated were volunteers from a pre-service mathematics teacher education course. Six students participated. The participants worked in the following pairs:
Pair I: James and Trisha. James and Trisha were paired by chance. Each of them had completed the mathematics requirements of the B. Ed. degree.
Pair II: Roger and Marie. Roger and Marie were paired by chance. Each of them had completed the mathematics requirements of the B. Ed. degree.
Pair III: Laura and Donald. Laura and Donald were paired by chance. Each of them had completed the mathematics requirements of the B. Ed. degree.
5. Other Studies
Sandy
In the winter of 1993-1994 several interviews were done with Sandy, a mathematically gifted student in grade 6. In one of these sessions Sandy was given the Arithmagon problem to explore. This session differed from the typical problem sessions as Sandy was questioned about his reasoning as he worked on the problem.
Central High School
In May 1993 I spent two weeks observing two mathematics classes at an academically oriented high school, as a preliminary study to the school studies. One of the classes observed was a grade 10 class studying linear equations. The other was a grade 11 International Baccalaureate class studying combinatorics and probability. The organization of the classes was flexible, but a typical period would begin with a lecture by the teacher, followed by work on assigned exercises, either individually or in small groups. Occasionally a period would begin with a problem solving exercise, to be done individually and as quickly as possible.
6. Methods
Three contexts for research were used in the studies. Different methods were appropriate for each of these. The classroom observations, and observations of the problem sessions involved passive observation techniques. The interviews employed techniques from traditional clinical interview methods (see below). All of these methods were used in the context of the Enactivist methodology described in Chapter VII.
The observers’ role in the observations of the problem sessions can be called ‘passive’, as the observers interrupted the participants’ work only when asked to do so by the participants. This usually took the form of the participants asking a factual question of the observers. This passivity permitted the students participating to ‘own’ the situation to a greater extent than in the interview sessions. Their explorations and interactions were governed more by their own interests and needs, than by those of the observers. In some of the problem sessions it is clear
that the number of observer interruptions is related to the degree to which the participant reasoned and understood in a connected manner (see Kieren, Pirie, and Reid, 1994, for details).
The clinical interview is a research method derived from the work of Piaget. Piaget developed the clinical interview in order to investigate reasoning in young children. The method has since been modified in many ways, involving more or less standardization. Opper (1977) gives this description:
The essential character of the method is that it constitutes a hypothesis-testing situation, permitting the interviewer to infer rapidly a child’s competence in a particular aspect of reasoning by means of observation of [the child’s] performance at certain tasks.... The interviewer presents to the child an “experiment” that has been selected as suitable for the study of the specific aspect of cognition of interest.... [The interviewer] asks a series of related questions which are aimed at leading the child to predict, observe, and explain ... It is these predictions, observations and explanations that provide useful information on the child’s views of reality and his thought processes. The verbal explanations are particularly valuable for inferring the underlying mental processes ... If further clarifications are required [the interviewer] asks additional questions or introduces extra items.... The information at any point may substantiate or invalidate the original hypothesis. In the former case, the interviewer may ask additional questions so as to satisfy himself of the stability and consistency of the child’s responses ... If the original hypothesis is not confirmed, the interviewer reformulates it to take into account the child’s responses and asks further questions or introduces additional items to clarify these responses. (pp. 92-93)
In the case of the interviews in my studies the “experiment” presented to the students were questions, notes and transcripts based on my previous observations.
7. Prompts
The situations the participants explored resemble those employed in problem solving research (e.g., Schoenfeld, 1985). While this research owes much to traditional problem solving research, the underlying assumptions concerning the nature of the participants’ activities differ. What would otherwise be seen as “problem solving” is seen here as a process of transforming a text (the prompt) into a situation and investigating and extending that situation. This process depends as much on the participants’ histories as it does on the originating text. Within this process we see both the participants’ cognitive structures being modified through learning about the situation, and also the situation itself being modified through interaction with the participants’ cognitive structures. Thus, these situations can be seen as co-emerging* with the participants during the course of a session.
The mathematical situations explored were based on three “prompts”; the texts on which the participants founded their explorations. Two of these,
* See Chapter VII for a description of co-emergence, and structure.
Arithmagon and Fibonacci, are traditional paper and pencil problems. The third is a LOGO microworld.
Arithmagon
The Arithmagon situation is derived from a problem in Mason, Burton, & Stacey (1985). The text used in the North School study was slightly different from the text used at South School, and in the clinical studies. The prompt used at North School was:
The numbers on the sides of this triangle are the sums of the numbers at the corners. Find the secret numbers.

Make up a triangle of your own, and solve it.
Can you describe a general way to solve all triangles?
Make up a square and solve it.
Can you find a general way to solve all squares?
The last four lines were replaced by the instruction “Generalize the problem and its solution” in the other studies. The questions were added to the North School prompt to try to focus the participants’ investigations along paths which I thought at the time to be the most fruitful. I do not believe this was the case, and so the prompt reverted to its original form for the second clinical and the South School studies.
Fibonacci
The prompt for the Fibonacci problem was modified for each study. The prompt used in the first clinical study was:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
If you are familiar with the recursive rule defining the sequence write it down. If you are not, try to discover the rule.
Use the notation Fn to stand for the nth Fibonacci number. For example, F7 is 13 and F10 is 55.
Look for patterns which relate the index n to the Fibonacci number Fn. For example, is there anything special about Fn when n is a multiple of 3, or a multiple of 4, or prime?
The prompt used at North School was:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
Try to discover a rule which will tell you the next number in the sequence.
Is there anything special about every third Fibonacci number ( 2, 8, 34, ...)?
Is there anything special about every fourth Fibonacci number (3, 21, ...)?
The prompt used in the second clinical study was:
The Fibonacci sequence begins:
1, 1, 2, ...
and continues according to the rule that each term is the sum of the previous two (e.g., 1+1=2).
The Fibonacci sequence has many interesting properties.
Can you find an interesting property of every third Fibonacci number?
Can you find other interesting properties?
The Fibonacci prompt in all its forms had the problem of being too directive. The intention of the questions was to inspire investigations in particular areas known to be suitable for deductive reasoning. They usually resulted in superficial investigations, since the participants were quick to go on to the next question.
In both the Arithmagon and Fibonacci situations the participants are given an initial puzzle to solve. In the Arithmagon the puzzle is the determination of the secret numbers. In the Fibonacci situation the puzzle is determining the recursive rule defining the sequence or finding a pattern in every third Fibonacci number. These tasks are puzzles in that they have definite answers, and are well within the capabilities of the participants. The giving of initial puzzles was intended as a means of giving the participants’ investigations an initial basis, motivation and direction. This was more successful in the case of the Arithmagon than in the case of the Fibonacci numbers.
GEOworld
The LOGO microworld, called GEOworld, is created by a simple recursive program (reproduced below) which accepts three numerical parameters and produces a geometric figure. In this case no initial puzzle was proposed. The situation is not really suited to the construction of simple puzzles. Instead an initial prompt was given. In the clinical studies the example of GEO 100 100 2 was included in the instruction sheet (Figure 34 shows the output of this input). In the second school study the functions of the three parameters were described vaguely, and three examples were proposed: GEO 100 100 2, GEO 135, 100 -3, and GEO 15 25 1. These prompts do focus the participants on certain aspects of GEOworld, to the neglect of others, but it was possible to ignore them.
to geo :a :b :c
if :b <1 [stop]
fd :b
rt :a
geo :a :b-:c :c
lt :a
bk :b
end
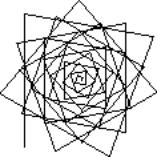
Figure 34: Output of GEO 100 100 3.
The Need to Prove
David A Reid
Page 145
To Beginning of appendix B | To End of appendix B