Proving to Explain
David A. Reid
University of Alberta
Abstract: It has been suggested that in teaching proving the explanatory potential of proofs and proving should be emphasized. My recent research has indicated that students are more likely to prove to explain than they are to prove to verify, but that there are important aspects of proving and explaining that must be considered; these include the degree of formulation of the proving, and the alternative of explaining by analogy.
IntroductionGila Hanna (1989) has suggested that teachers should be aware of the potential that proofs have of explaining as well as verifying mathematical statements. Others (e.g., de Villiers 1991, 1992) have conducted empirical studies which lend support to this suggestion. In my recent research I have been attempting to develop a clearer description of the reasons proving is used by students in problem solving. Chief among these reasons, or needs, are explaining, exploring, and verifying. A distinction between my work and that of Hanna and de Villiers, is that they referred to proofs which were presented to students as explanations, while I am more concerned with the explanatory power of the proving students do themselves. It should also be noted that I use ďprovingĒ to describe any deductive reasoning, even if no proof is produced.
Hanna described explaining in this way:
I prefer to use the term explain only when the proof reveals and makes use of the mathematical ideas which motivate it. Following Steiner (1978), I will say that a proof explains when it shows what ďcharacteristic propertyĒ entails the theorem it purports to prove. (p. 47)This characteristic, of revealing the underlying principles on which the proof rests, is undoubtedly a part of what makes proving a useful way of explaining for students.
This paper reports some results from my research into studentsí proving in problems solving which relate specifically to proving to explain. I will distinguish between formulated and unformulated proving to explain, and provide examples of proving of different degrees of formulation. I will also give an example of explaining by analogy which will illustrate the conflict between explaining by proving and explaining by analogy, under the influence of social constraints. I will conclude by describing some implications for the use and acceptance of explanations based on proving.
Formulation is one of the most important characteristics of proving when used to explain. Formulation refers to the knowledge or awareness, on the part of the prover, that s/he is proving.
Proving to Explain
David A Reid
Page 1
To Beginning of Article | To End of Article
It could also be described as the degree to which the proving is thought-of and thought-out. Formulation is related to two other characteristics of proving: its articulation, and the hidden assumptions made while proving. The extent and clarity of the spoken or written articulation of proving has implications both for the possibility of the proving being interpreted by others, and for the formulation of the proving. Being aware of oneís own proving, and being able to articulate that proving, are interrelated. Articulating proving assists in formulating, as articulation makes aspects of proving tangible. At the same time formulated proving is more easily articulated. All proving involves some hidden assumptions. These assumptions can range from wrong assumptions, through implausible and plausible assumptions, to assumptions which are known within a community. The formulation of proving reveals hidden assumptions, making the presence of wrong or implausible assumptions less likely. Articulation and hidden assumptions provide valuable clues to formulation, in addition to being important characteristics of proving in and of themselves.
Explaining in problem solvingThe results reported here are taken from a larger research project on proving, involving observations and interviews with high school and university students engaged in problem solving. The general object of this research project is the investigation of the needs which proving addresses for mathematics students. Other aspects of this project have been reported in Reid (1994), Kieren & Reid (1994), and Kieren, Pirie, & Reid (1994). The examples below are taken from problem solving session which involved four university students, Rachel, Eleanor, Ben, and Wayne, working on the Arithmagon problem (from Mason, Burton & Stacey, 1985; see Fig. 1). I will describe briefly the activities of the four participants, pausing to provide more detail and analysis of episodes of explanation.
A secret number has been assigned to each corner of this triangle. On each side is written the sum of the secret numbers at its ends. Find the secret numbers.
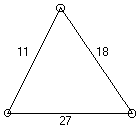
Generalize the problem and its solution.
Figure 1: The Arithmagon problem
Partially formulated proving to explain.
The four participants were seated at an ďLĒ shaped table in such a way that Rachel and Eleanor could easily work together, as could Ben and Wayne. Eleanor and Ben were seated closest to the bend in the table. Rachel and Eleanor began by setting up systems of equations and solving them. They arrived at the solution after about four minutes. Ben guessed the solution within 30 seconds of being given the prompt. He and Wayne then worked
Proving to Explain
David A Reid
Page 2
To Beginning of Article | To End of Article
independently, trying to find patterns in the solved puzzle. Ben concentrated on relations between the numbers, while Wayne attempted to make use of geometric properties of triangles.
Once everyone had a solution they compared notes. Although Ben initially claimed to have no idea how he had found the answer so quickly, he eventually reconstructed a plausible explanation (Long dashes, ó, indicate short pauses):
(A1) Ben: You know how I did that? The number here had to be less than 27, and less, it had to be less than 18, the numberhere, right, ó had to be less than 18. And the number here had to be less than 11,ó right?
Note that while there is a lot left out of his explanation, Ben is fairly articulate in explaining how one might limit the possible cases to a number small enough to make testing all of them feasible. The basis of the constraints, the justification for the use of ďhad to be,Ē is a deduction from a hidden, but plausible, assumption that the secret numbers are all natural numbers. This partially formulated proving to explain was fairly successful as such, although it left Eleanor and Rachel with a need to explore its workings in more detail. Benís later proving was less formulated, and less successful as explanation, as the next example will show.
Unformulated proving to explain
Rachel and Eleanor tried to use Benís method to solve another triangle, and tried to see if there are other constraints that would help them determine the secret numbers exactly. Ben watched their efforts, and after a few minutes he claimed that any triangle could be solved by his constraints method. In an effort to make him aware of his assumption that only natural numbers could be used, I suggested that he solve a triangle with the values 1, 4, and 12 on the sides (The secret numbers are 7.5, 4.5, and Ė3.5).
(B1) Ben: On the sides, 1, 4, 12. Well that's 0 or 1. One of them has to be 0 - No, That's impossible - Because, I mean if this one is 0, that one has to be 1, that one has to be 3, this adds up to 3. If this one is 0, this one has to be 4 and that one has to be 1.
(B2) Wayne: Who said it's got to be 0 though?
(B3) Ben: Well, Yeah - It still shouldn't matter - if you go down on the number line you still have to go up on the number line.
Benís initial comments (B1) are similar to those quoted above, in line A1. He explains why the triangle is impossible, by reasoning deductively from the implicit assumption that the secret numbers are natural numbers. When Wayne questions his hidden assumption, Ben immediately offers further explanation (B2). Note that this explanation has a different character from the ones he has offered before (A1 & B1). It is much less articulated, making it difficult to judge how aware Ben was of his reasoning. His language suggests that his proving is based on an image of the relationship between the values. These features lead me to characterize this explanation as unformulated proving.
Unformulated proving is not very useful as explanation, as is illustrated by Benís continuing attempts to explain: (C1) Eleanor: But this doesnít have to be 0Proving to Explain
David A Reid
Page 3
To Beginning of Article | To End of Article
(C2) Ben: But even if it is, like letís say negative 4 and negative 3, right? You still have to get this to be 4 it has to be 7, all right? Itís still minus. So it will still be like, 3. ó You know where Iím coming from?
(C3) Eleanor: Say it again.
(C4) Ben: The difference, the difference between these two is still always going to be 1, right? No matter if you represent it with negative or adding.
Eleanorís request to ďsay it againĒ marks the failure of Benís unformulated proving to explain to her. Ben has based his argument (in C2) on a hidden assumption, which in this case is wrong. He seems to believe that the difference between the two secret numbers is 1. This is true in the case where one of them is zero, which he had just been considering. The two numbers he names, Ė4 and Ė3, have a difference of 1, and these numbers do not work. In fact, if the difference must be 1, there is no way that a difference as large as (12Ė4) could occur. This provides the basis for Benís belief that the puzzle can not be solved.
Ben seems determined to explain why the triangle has no solution. There are several needs interacting in this case. In order to convince Eleanor, he needs to be able to explain the situation to her, and to do so he needs to explore it more thoroughly than he had to in order to verify for himself that it could not be solved. His failure to convince Eleanor had the effect of undermining his verification, which caused him to shift from explaining what he had verified to Eleanor, to exploring the now reopened question of whether of not the triangle could be solved. Benís unformulated proving did not work as an explanation for Eleanor, in spite of her willingness to listen carefully, and to work through Benís ideas. The next example shows how Eleanorís receptiveness and Rachelís ability to formulate her proving combined to produce an explanation.Formulated proving to explain
Eleanor, Ben, and Wayne continued to work together,
exploring the situation inductively. They
discovered two interesting properties: 1) The sum of the numbers on the sides is twice the sum of
the secret numbers; (a+b+c)
= 2(x+y+z).
2) The sum of a secret number and the number on the opposite side is
the same for all the secret numbers; (a+x)
= (b+y) = (c+z).
During this time Rachel had been working independently, exploring using
algebraic derivations. After
twenty minutes Rachel announced that she had found a formula:
![]() . Ben and Wayne immediately began
to verify it inductively, but Eleanor asked for an explanation, ďHow did you
get that?Ē
. Ben and Wayne immediately began
to verify it inductively, but Eleanor asked for an explanation, ďHow did you
get that?Ē
| Transcript | Rachel's Writing |
| (D1) Rachael: X plus Y equals A
(D2) Elanoer: Yeah |
(2) y + z = b (3) z + x = c
|
| (D5) Rachel: and then just add A and - Add the first two
equations.
(D6) Eleanor: Yeah |
|
Proving to Explain
David A Reid
Page 4
To Beginning of Article | To End of Article
| (D7) Rachel: This. - That's right, right? That's
what I got?
(D8) TK: Work it through cleanly for her. |
|
| (D9) Rachel: Oh, Ok. So, 1 plus 2 is X plus Y equals
A, Y plus Z- Did I add?
(D10) TK: Yeah. (D11) Rachel: Oh it doesn't matter which two you add up. |
x + 2y + z + a + b |
| (D16) Rachel: But, X plus Z is C, right?
(D17) Eleanor: Right. (D18) Rachel: So - (D19)Together: -2Y plus C- |
2y = a + b - c |
Rachelís explanation to Eleanor is quite formulated. She articulated her steps clearly, both in her writing and her speech. She was aware of the structure of her own reasoning, as is indicated by her observation that she is free to choose any pair of equations to add together (D11). Her only hidden assumptions are the basic rules of algebra and arithmetic which she can safely assume are known to and shared by Eleanor.
One might expect that Rachelís formulated proving would be the preferred form of explanation for this group. The next example shows that this was not so, and indicates the importance of both the clarity of the explanation, and the receptiveness of those to whom it is offered, to the acceptance of an explanation.
Explaining by analogy versus explaining by proving
After Ben and Wayne had verified Rachelís formula, and Rachel had explained it to Eleanor, Wayne wondered why it is necessary to divide by 2. Ben, Rachel, and Wayne all offered explanations:
(E1) Ben: You know why you divided by 2, is because-
(E2) Rachel: Because thereís two sides.
(E3) Ben: No. No, itís because-
(E4) Wayne: Thereís two other points, to be solved for, no?
(E5) Ben: No. No. No. We found out that Y, X + Y + Z is half of the outside points.
(E6) Wayne: Thatís right!
Rachelís explanation (E2) for the division by 2 is quite correct, and based on the proving she had done in deriving her formula. The brief statement she was able to make was not, however,
Proving to Explain
David A Reid
Page 5
To Beginning of Article | To End of Article
sufficient to communicate anything to Ben and Wayne. Even though her statement did not explain anything to Ben and Wayne, I would consider it to be an example of using formulated proving to explain. The proving, however, was all done ahead of time, and she merely assumes it in her explanation.
Wayneís explanation (E4) is an example of an explanation by means of a weak analogy. The number 2 is involved both in the division by 2, and in the number of vertices to be solved, once the first is known, but that is the only connection between them. It is interesting that, even though Wayne had been the first to voice a need to understand the division by 2, but at this point he seems more anxious to suggest his own explanation than to hear Benís.
Benís explanation (E5) is a strong analogy. The analogy is between two equations with variables, instead of between an equation and a state of affairs (as in the case of Wayneís analogy). This strength is likely to have led to Wayneís acceptance of Benís explanation over his own (E6). Ben is referring to the relationship a+b+c = 2(x+y+z), which he had discovered inductively with Eleanor and Wayne (see above).
The explanations which were rejected were a weak analogy (Wayneís, E4) and a deductive explanation which could be taken to be a weak analogy (Rachelís, E2). The students preferred the strong analogy, which was based on several points of connection. This is sensible, as a strong analogy could have (and in this case does have) the potential to be developed into a deductive proof.
It is worth noting that even though Rachelís explanation was the most thought out, and based on deduction rather than analogy, which might suggest it was a more certain explanation, it was apparently not even considered by the others. This illustrates a weakness of proving versus analogy for explaining. Proving is a process which must be formulated to be communicated, and must be followed with some care to be understood. In this situation the social dynamic did not afford Rachel the opportunity to make her case clearly. Benís analogy (E5), on the other hand, could be understood immediately by Wayne and Eleanor, who were familiar with the context to which he was making links. Rachel could also see these links after Eleanor showed her the formula which was being referred to.
Conclusions
The examples above illustrate the range of formulation which proving to explain can cover. While Hanna (1989) points out that some proofs are so formal that they do not explain, proving can also fail as explanation because it is not sufficiently formulated. Further, proving to explain has disadvantages compared to explaining by analogy, in contexts where articulation of the proving is difficult.
The deductive explanations described above involve both unformulated proving and formulated proving. They show that unformulated proving is not very successful in explaining to others, although it might be explanatory to the person proving. Unformulated proving lacks the quality of clarity, which explanation to others requires. Formulated proving is more successful as a way of explaining. Its main weakness is the time and attention it requires of the
Proving to Explain
David A Reid
Page 6
To Beginning of Article | To End of Article
listener. This can make it useless as explanation in social contexts which do not allow for extended explanations.
The main rival of proving for explaining is the use of reasoning by analogy. Explaining by analogy is more or less successful, depending on the strength of the analogy. A strong analogy might be accepted in preference to a deductive explanation. A weak analogy, however, seems to leave room for a better explanation by formulated proving. Some explanations by analogy make connections which could be established deductively, as was the case when Ben explained the division by 2 in Rachelís formula (E5). It should be noted, however, that I have yet to observe students attempting to transform an analogy in this way. The question of the relationship between analogy and deduction could be a useful focus of further research.
In thinking about explanation it is essential to keep in mind that more than the intent to explain is required for the success of an explanation. Any means of explanation must also involve articulation of sufficient clarity to allow others to understand it. In addition those others must be willing to devote the time and attention necessary to understanding the explanation. It is the combination of these factors which makes an explanation, and which puts certain constraints on the circumstances in which proving can be explaining.
References
de
Villiers, M. (1991). Pupils' need for conviction
and explanation within the context of geometry. Pythagoras,
No. 26, 18-27.
de
Villiers, M. (1992). Children's acceptance of theorems in geometry.
Poster presented at The Sixteenth Annual Conference of the
International Group for the Psychology of Mathematics Education, Durham NH.
Hanna,
G. (1989). Proofs that prove and proofs that explain. In Proceedings of the
Thirteenth International Conference on the Psychology of Mathematics
Education, (pp. 45-51). Paris.
Kieren,
T., Pirie, S. & Reid, D. (1994). Mathematical
understanding: Always under construction.
In J. da Ponte & J. Matos, (Eds.),
Proceedings of the Seventeenth Annual
Conference of the International Group for the Psychology of Mathematics
Education, (Vol. 4, pp. 49-56). Lisbon.
Kieren,
T. & Reid, D. (1994). Portraying
the growth of mathematical understanding: Understanding and deductive
reasoning in mathematical activity. A
paper presented at the Annual Meeting of the Canadian Society for the Study of
Education. Calgary.
Mason J., Burton, L., & Stacey, K. (1985). Thinking Mathematically. New York: Addison Wesley.
Reid, D. (1994). "Why 4?": Explanations in mathematical problem solving. A paper presented at the Annual Meeting of the Canadian Society for the Study of Education. Calgary.
Steiner, M. (1978). Mathematical explanation. Philosophical Studies, 34, 135-151.
Proving to Explain
David A Reid
Page 7
To Beginning of Article | To End of Article