CONSTRAINTS AND OPPORTUNITIES IN TEACHING PROVING
David A. Reid
Memorial University of Newfoundland
Abstract: Analysis of reasoning taking place in classrooms involves more than consideration of the forms reasoning takes and the needs which motivate it. The curriculum, didactic contracts, and culture of the classroom constrain what reasoning can occur. At the same time, discovery activities and opportunities for discourse can provide occasions for reasoning. This paper briefly considers the interplay of these constraints and occasions in a Canadian grade 10 classroom.
In previous research (Reid 1995 a,b) I developed a vocabulary for describing deductive reasoning. This research was based on clinical interviews with secondary school and university students engaged in open ended problem solving. Recently I have been attempting to apply this vocabulary to describing the deductive reasoning of secondary students in their classrooms. In so doing I have also seen the effects of applying classroom cultures to my vocabulary. In the following I will describe these experiences in terms of occasions for, and constraints on, deductive reasoning in a secondary school classroom.
Background on enactivism and evolution
Over
the past few years I have been exploring, with other members of the enactivism
research group, the ways in which ideas derived from Maturana and Varela’s
enactivist theory of cognition (Maturana & Varela 1992; Varela, Thompson
& Rosch 1991) can be applied to the learning of mathematics.
We have addressed such ideas as the coemergence of learners in a
problems solving situation (Kieren, Gordon Calvert, Reid & Simmt 1995),
ways of describing proving (Reid 1995 a, b), the nature of teaching (Kieren,
Gordon Calvert, Reid & Simmt 1996), and research methodology (Reid 1996a).
I will be using enactivist ideas here to describe students’ proving
in classroom contexts.
An
important idea in enactivism is that of satisficing.
This idea is derived from theories of evolution which posit that
organisms do not evolve to optimal states, but rather any form which is not
fatally detrimental continues to be propagated.
In such a view the organism’s environment does not determine
the form of the organism, but it does offer constraints
which shape the organism by disallowing certain forms.
In classroom teaching the idea of satisficing can be applied to mathematical behaviours. The teacher’s actions and the classroom context do not determine what mathematical behaviours the students will evolve, but they offer constraints which disallow certain forms. In practice the forms of behaviour which are allowed are
David A Reid
Page 1
likely
to exceed the bounds intended by the teacher, because of the interplay of
factors involved in classroom contexts.
In
describing what teachers do in classrooms we consider teaching to be providing
opportunities for learning. Because
students’ learning is determined by their own structures the opportunities
created by a teacher cannot “cause” students to learn.
When learning does take place we call the opportunities created by the
teacher “occasions.”
Proving
as explaining
The
classroom context which I will describe here is that of a Canadian grade 10 (≈15
years old) middle stream mathematics class.
My observations covered three months of instruction, involving problem
solving and group work on graphs of linear equations and Euclidean geometry.
The class used materials which I prepared in consultation with their
classroom teacher, which had been tested in a pilot study the previous year (Blackmore,
Cluett & Reid 1996). The
materials encouraged students to explain aspects of graphing linear functions,
and theorems in Euclidean geometry. The
teaching methods employed provided students with opportunities to learn to
communicate mathematically, and to work cooperatively in mathematical
situations.
In
my descriptive vocabulary proving is considered to be in response to one of
four needs: to explain, to explore, to verify, and as part of a social
process. As the importance of
proving to explain has been emphasized in recent research (Hanna 1989, 1995;
de Villiers 1991, 1992), explaining was presented as the primary motive for
proving in the activities used in the class.
Students were encouraged to use deductive
reasoning to explain mathematical propositions, and proving in this context
meant explaining deductively.
Opportunities:
discourse, discovery, debate.
Previous
research has suggested that it is through guided exploration and class
discussions that students can best learn to reason deductively (Balacheff,
1991; Lampert 1990; Fawcett 1938). On
most days the class’s activities allowed for a great deal of exploration and
discussion. Prompts were given which presented a situation and asked for
an explanation. These prompts
were worked on in small groups (2-5 students per group) and group conclusions
were presented to the whole class. The
assumption was made that this pattern would be an opportunity for students to
explain deductively, and to express and clarify their reasoning through social
interaction.
The
students' discussions often occasioned short explanations, which were
sometimes deductive. One prompt
which occasioned some extended reasoning was: “In general two lines which
are perpendicular have slopes which are negative reciprocals. Why?
The following example may help. [The graphs of y=
![]() x and y=-
x and y=-
![]() x were given]” In one group the
students observed that the triangle they had drawn to show the slope was
rotated 90 degrees. They then
used this observation to conclude
x were given]” In one group the
students observed that the triangle they had drawn to show the slope was
rotated 90 degrees. They then
used this observation to conclude
David A Reid
Page 2
that
because the triangles were rotated the rise indicated by one would be equal to
the run of the other, and vice versa.
Many
discoveries were occasioned by the prompts given the students.
These ranged from procedures to determine equations of lines, to
definitions of geometrical terms, to congruencies related to transversals of
parallel lines. In some cases
students made discoveries which had not been anticipated by their teacher and
me. For example in explaining why
two triangles were congruent in a particular diagram, they observed that the
triangles formed a parallelogram and asserted their congruence based on the
congruency of the opposite sides.
The
process of social debate was especially valuable during the unit on deductive
geometry. In the course of
addressing the questions of their peers, their teacher, and myself, the
students clarified and formulated their arguments.
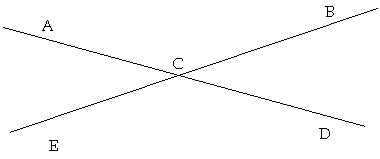
One pair presented the following to the class:
|
A)
Which angles are congruent? Why? |
|
||
|
–ACB@–DCE –ACE@–DCB
|
|
||
|
—
Two angles that have the same measures are congruent. |
|
||
In
the ensuing debate they were asked how they knew the angles had the same
measure. Other members of the class asserted that they had the same
measure because they were “vertically opposite.” This was something they remembered from the previous year.
As
“vertically opposite” had not been defined previously, the class paused to
discuss a suitable definition, arriving at “Two angles that have the same
vertex and the opposite rays from the opposite angle form a straight line.”
While this is not the most elegant definition, it has the advantage
that everyone in the class understood it and accepted it, and it had been
carefully thought about by the students themselves.
Once
this was settled the pair presenting amended their statement to read: “—
Two angles that have the same measures are congruent. because they are
vertically opposite.”
One of the roles I played in the class was to ask “Why?” In this case this occasioned a debate concerning why vertically opposite angles have the same measure. Several members of the class were actively engaged in this debate, contributing suggestions for ways of expressing ideas and new approaches. One student suggested several
David A Reid
Page 3
verbal
explanations, and with the help of several classmates arrived at this written
formulation: “two angles that have a common angle to make them supplementary
have to be equal.” Again the
language is strained, but the students understood its meaning, and accepted it
because it embodied the reasoning they had gone through.
Constraints:
curriculum, contracts, culture.
Although
the students’ use of opportunities as occasions for learning was
encouraging, even more evident were the constraints which kept them from
reasoning deductively. These
included the official and traditional curricula, the roles of the teacher and
students, and the classroom culture.
Some
objectives in Unit I: Linear Sentences of the provincial curriculum
(Government of Newfoundland and Labrador, 1993) acted as a constraint on the
students’ reasoning. Objectives
1.6: “Students will be expected to rewrite linear equations.” (p. 17)
and 1.7: Students will be expected to graph a linear equation using
various methods” (p. 18) are typical in their focus on algebraic
manipulation and skill. The
amount of time needed to develop the students’ algebraic skill to the
required level limited the amount of time which could be devoted to developing
a deductive structure for the coordinate plane.
The short time allotted to the deductive geometry unit in the
provincial curriculum also acted as a constraint as it precluded a thorough
discussion of the properties the students discovered in their explorations.
In
addition to the official curriculum, there is also a traditional curriculum
which acts as a constraint on reasoning.
The official curriculum objectives for the Deductive Geometry unit
explicitly state that “the overall objective is for students to be able to
produce proofs” (p. 26). The
text used for the course, however, adds an additional objective, that students
be able to reason in geometric contexts using algebraic language. A typical*
textbook exercise is this:
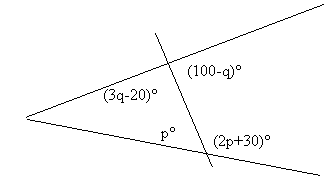
(Ebos,
Morrison, Spinney & Dalton, 1992, p.319)
Similar exercises are also traditionally a part of the year end examinations. In such exercises students are expected to determine the measures of the angles by solving equations. For the most part the students had no trouble setting up the equations based on the geometric properties of the figure. Solving the equations and making
* This exercise is only atypical in that the diagram contradicts the information given. This led to a useful discussion.
David A Reid
Page 4
sense
of the result were their main difficulties.
The experience of struggling through solving an equation was
frustrating to most of the students, and limited the time and mental energy
they had to engage in more sophisticated reasoning.
Laborde
(1989) describes didactic contracts
(originally named by Brousseau, 1980): the asymmetrical roles assigned to
teachers and students as a result of the differing knowledge they bring to the
classroom. As in many classrooms
the contract tacitly agreed at the beginning of the school year called for the
teacher to demonstrate mathematical procedures and for the students to copy
them. In expecting the students to discover mathematical procedures and
principles their teacher violated this contract, and the students reacted by
being uncooperative for the first week. As
the students came to understand their new roles the contract was effectively
renegotiated, and the students became more cooperative. In times of stress,
however, both teacher and students returned to more familiar roles and
patterns of activity. The
original contract continued to influence what was possible in the classroom.
Lampert (1990) has emphasized the importance of developing a classroom culture in which students feel at ease proposing conjectures and defending them. For many of the students in the class involved in my study, they had not experienced such classroom cultures in previous years, and did not expect to be a part of one. The tension between the teachers’ use of her authority to maintain order in the class room and the intent to provide students with autonomy served to undermine the development of a culture of mathematical respect. Some were willing to participate in debates and discussions in a way which fit the developing culture, but others felt intimidated, and were not willing to state a conjecture unless they knew they were correct.
Teaching
proving: ideas for the future.
It is not a new observation that mathematical reasoning in classrooms depends as much on social factors as on psychology. In looking for ways to expand my descriptions of reasoning I was not surprised to find myself considering the social dynamics of the classroom — only the extent to which constraints kept deductive reasoning from happening. The claims I had heard teachers make that their students did not reason deductively began to make more sense to me.
Considering the social context from the pint of view of reasoning satisficing needs to explain, explore and verify (as opposed to satisfying those needs) let me connect the enactivist ideas of constraints and occasions to my existing structure of needs to and forms of reasoning mathematically.
I am now engaged in elaborating these connection and preparing to add the new perspective this gives me to those through which I have researched reasoning in the past. what I hope for is a multifaceted perspective including a multiplicity of mutually intelligible but distinct points of view, and the consideration of constraints and opportunities in making sense of students’ mathematical behaviour.
Constraints and Opportunities in Teaching
Proving
David A Reid
Page 5
To Beginning of Article | To End of Article
References
Balacheff, N. (1991). The benefits and limits of social interaction: The case of mathematical proof. In A. Bishop, S. Mellin-Olson, & J. van Doormolen (Eds.), Mathematical knowledge: Its growth through teaching (pp. 175-192). Boston: Kluwer Academic.
Blackmore, D., Cluett, G., & Reid, D. (1996). Three perspectives on problem-based mathematics learning. In Jakubowski, E., Watkins, D., and Biske, H. (eds.) Proceedings of the Eighteenth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. (Vol. 1, pp. 258-262) Columbus OH: ERIC Clearinghouse for Science Mathematics, and Environmental Education.
Brousseau, G. (1981). Problèmes de didactique des decimaux. Recherches en Didactique des Mathématiques, 2.1, 37-125.
de Villiers, M. (1991). Pupils’ need for conviction and explanation within the context of geometry. Pythagorus, n. 26, 18-27.
de Villiers, M. (1992). Children's acceptance of theorems in geometry. Poster presented at The Sixteenth Annual Conference of the International Group for the Psychology of Mathematics Education, Durham NH.
Ebos, Morrison, Spinney & Dalton. (1992). Mathematics 10: Principles and process. Scarborough, ON: Nelson.
Fawcett, H. P. (1938). The nature of proof: a description and evaluation of certain procedures used in a senior high school to develop an understanding of the nature of proof. (NCTM yearbook 1938) New York: Teachers' College, Columbia University.
Government of Newfoundland and Labrador (1993). Mathematics 1300 curriculum guide. St. John’s: Government of Newfoundland and Labrador.
Hanna, G. (1989). Proofs that prove and proofs that explain. In Proceedings of the Thirteenth International Conference on the Psychology of Mathematics Education, (pp. 45-51). Paris.
Hanna, G. (1995). Challenges to the importance of proof. For the Learning of Mathematics, 15(3), 42-49.
Kieren, T., Gordon Calvert, L., Reid, D. & Simmt, E. (1995). An Enactivist Research Approach to Mathematical Activity: Understanding, Reasoning and Beliefs. Presented at the Annual Meeting of the American Educational Research Association, San Francisco.
Kieren, T., Gordon-Calvert, L., Reid, D. & Simmt, E. (1996). Occasioning: Learning in the interaction. Presented at the Annual Meeting of the American Educational Research Association, New York.
Laborde, C. (1989). Audacity and reason: French research in mathematics education. For the Learning of Mathematics, 9(3), 31-36.
Constraints and Opportunities in Teaching
Proving
David A Reid
Page 6
To Beginning of Article | To End of Article
Lampert, M. (1990). When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. American Educational Research Journal, 27(1), 29-63.
Maturana, H., & Varela, F. (1992). The tree of knowledge: The biological roots of human understanding. Boston: Shambala.
Reid, D. (1995a). The need to prove. Unpublished doctoral dissertation, University of Alberta, Department of Secondary Education.
Reid, D. (1995b). Proving to explain. In L. Meira & D Carraher, (Eds.), Proceedings of the Nineteenth Annual Conference of the International Group for the Psychology of Mathematics Education, (Vol. 3, pp. 137-143). Recife, Brazil.
Reid, D. (1996a). Enactivism as a methodology. In L. Puig & A Gutiérrez,(Eds.), Proceedings of the Twentieth Annual Conference of the International Group for the Psychology of Mathematics Education, (Vol. 4, pp. 203-210). Valencia, Spain.
Reid, D. (1996b). The role of proving: Students and mathematicians. Presented to Topic Group 8: Proofs and proving: Why when and how. Eighth International Congress on Mathematical Education, Sevilla.
Varela, F., Thompson, E., & Rosch, E. (1991). The embodied mind: Cognitive science and human experience. Cambridge MA; MIT Press.
Constraints and Opportunities in Teaching
Proving
David A Reid
Page 7
To Beginning of Article | To End of Article